ЕГЭ профиль № 18
Монеты

У Миши в копилке есть 2-рублевые, 5-рублевые и 10-рублевые монеты. Если взять 10 монет, то среди них обязательно найдётся хотя бы одна 2-рублевая. Если взять 15 монет, то среди них найдётся хотя бы одна 5-рублевая. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 10-рублевая.

а) Может ли у Миши быть 30 монет?

б) Какое наибольшее количество монет может быть у Миши?

в) Какая наибольшая сумма рублей может быть у Миши?

Решение:

Из условия понятно, что у Миши минимум 20 монет.

Рассмотрим 1 условие: если взять 10 монет, то среди них обязательно найдётся хотя бы одна 2-рублевая.  И начнём прибавлять по 1 монете к общему числу монет.

Среди 10 монет будет обязательно одна 2-рублевая, среди 11 монет – две, среди 12 монет – три и т.д.

Пусть 2-рублевые монеты зеленого цвета, 5-рублевые – оранжевого, 10-рублевые – желтые. Белые кружки – любая монета.

В общем случае условие можно записать следующим образом:

(х – 9) – минимальное количество 2-рублевых монет, где х – общее число монет.

Продолжим добавлять по 1 монете к общему числу монет. Так как монет уже 15 и больше, то добавляем 5 – рублевые монеты. Для 5-рублевых монет условие аналогичное:

(х – 14) – минимальное количество 5-рублевых монет, где х – общее число монет

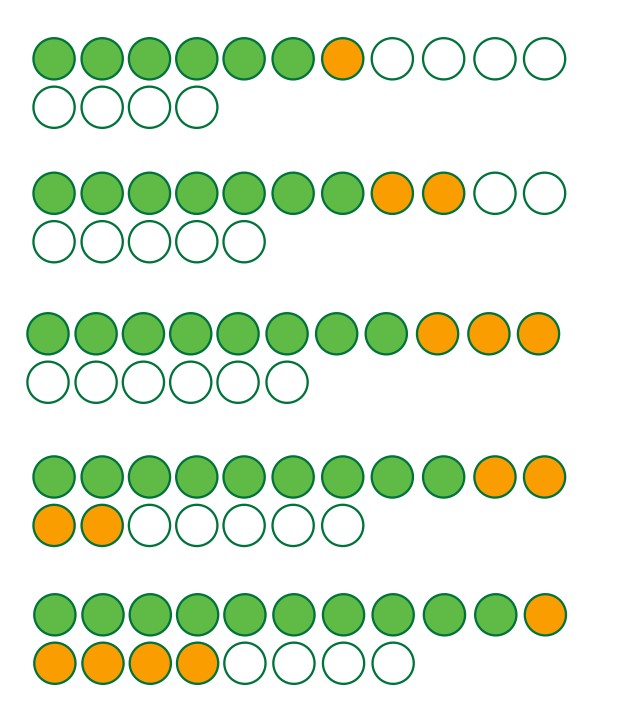
Начинаем добавлять 10-рублевые монеты.

(х – 19) –  минимальное количество 10 -рублевых монет, где х – общее число монет

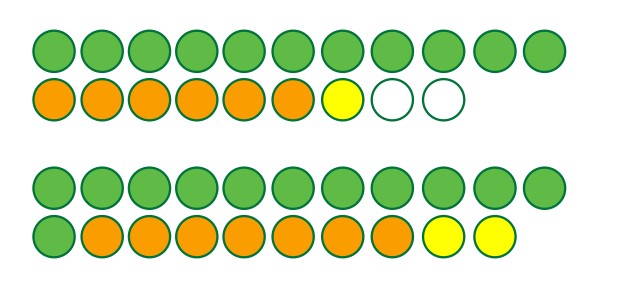
Если добавить еще 1 монету, то условие задачи выполнено не будет. Мы видим, что максимальное количество монет – 21.

а) нет, так как максимальное количество монет – 21.

Можно рассмотреть альтернативное решение:

Известно, что (х-9) – минимальное количество 2-рублевых монет. Значит, 2-рублевых монет будет минимум (30-9) = 21

Минимальное количество 5-рублевых монет: (30-14) = 16

Минимальное количество 10-рублевых монет: (30-19) = 11

Значит, минимальное количество 2-рублевых, 5-рублевых и 10-рублевых – (21+16+11) = 48 > 30 –противоречие.

б) 21

Мы знаем, что у Миши минимум 20 монет.

Пусть у Миши 21 монета. Тогда:

Минимальное количество 2-рублевых монет (21-9) = 12

Минимальное количество 5-рублевых монет (21-14) = 7

Минимальное количество 10-рублевых монет (21-19) = 2

Значит, минимальное количество 2-рублевых, 5-рублевых и 10-рублевых – (12+7+2) = 21.

Пусть у Миши 22 монеты. Тогда:

Минимальное количество 2-рублевых монет (22-9) = 13

Минимальное количество 5-рублевых монет (22-14) = 8

Минимальное количество 10-рублевых монет (22-19) = 3

Значит, минимальное количество 2-рублевых, 5-рублевых и 10-рублевых – (13+8+3) = 24 > 22 – противоречие.

Значит, максимальное количество монет у Миши – 21.

в) У Миши может быть либо 20 монет, либо 21. Посчитаем, какая наибольшая сумма рублей может быть у Миши.

Если у Миши 21 монета, то у него 12 2-рублевых монет, 7 5-рублевых и 2 10-рублевых. Значит, у него будет (12*2+7*5+2*10) = 21+35+20 = 76 рублей.

Если у Миши 20 монет, то у него 11 2-рублевых, 6 5-рублевых и 1 10-рублевая. Плюс у него может быть еще 2 любые монеты. Чтобы сумма была максимальной, добавим ему еще 2 10-рублевые монеты. Значит, у него будет (11*2+6*5+3*10) = 22+30+30 = 82 рублей.

Тогда наибольшая сумма рублей у Миши – 82 рубля.

Ответ: а) нет; б) 21; в) 82