ЕГЭ профиль № 6
Площадь под графиком функции

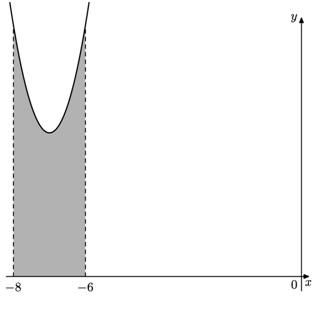
На рисунке изображён график некоторой функции y = f(x). 

Функция F(x) = x3 + 21x2 +151x — 1 — одна из первообразных функции f(x). 

Найдите площадь закрашенной фигуры. 

Решение:

Площадь под графиком функции f(x) на отрезке [a; b] равна разности первообразных:

S = F(b) — F(a)

Нам необходимо найти площадь закрашенной фигуры на отрезке [-8; -6], то есть  a = -8; b = -6. Значит S = F(-6) — F(-8).

Найдем F(-8):

F(-8) = (-8)3 + 21⋅(-8)2 +151⋅(-8) — 1

F(-8) = — 512 + 21⋅64 — 151⋅8 — 1

F(-8) = — 512 + 1344 — 1208 — 1

F(-8) = — 513 + 136

F(-8) = -377

Найдем F(-6):

F(-6) = (-6)3 + 21⋅(-6)2 +151⋅(-6) — 1

F(-6) = — 216 + 21⋅36 — 151⋅6 — 1

F(-6) = — 216 + 756 — 906 — 1

F(-6) = — 217 — 150

F(-6) = -367

Тогда площадь закрашенной фигуры равна:

S = F(-6) — F(-8) = -367 — (-377) = -367 + 377 = 10

Ответ: 10