Правильный шестиугольник

Вам тоже становится страшно, когда вы видите в условии задачи «правильный шестиугольник»? Вам хочется сразу перейти к другой задаче? Вы не знаете, как с ним работать ?

 ? Страх перед задачами подобного рода возникает по простой причине — незнание свойств правильного шестиугольника. Ознакомившись с ними, вы с легкостью будете решать задачи с шестиугольниками. В них нет ничего сложного. Давайте разбираться.

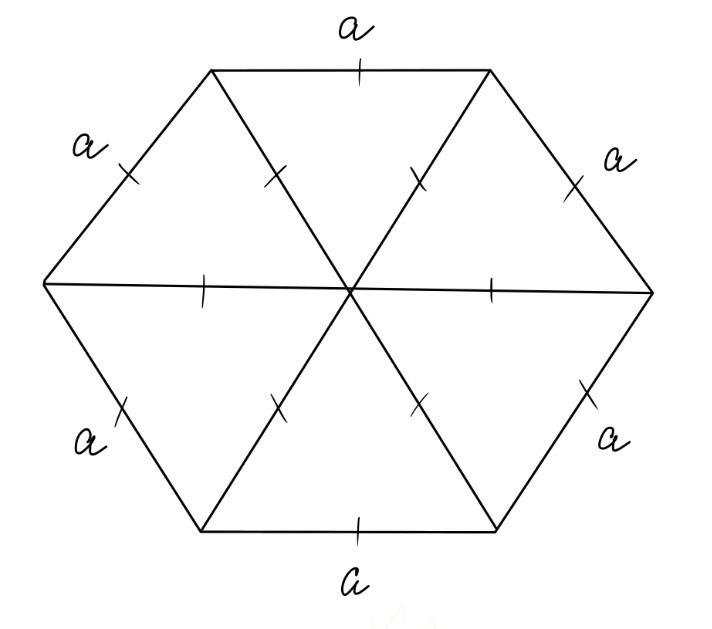
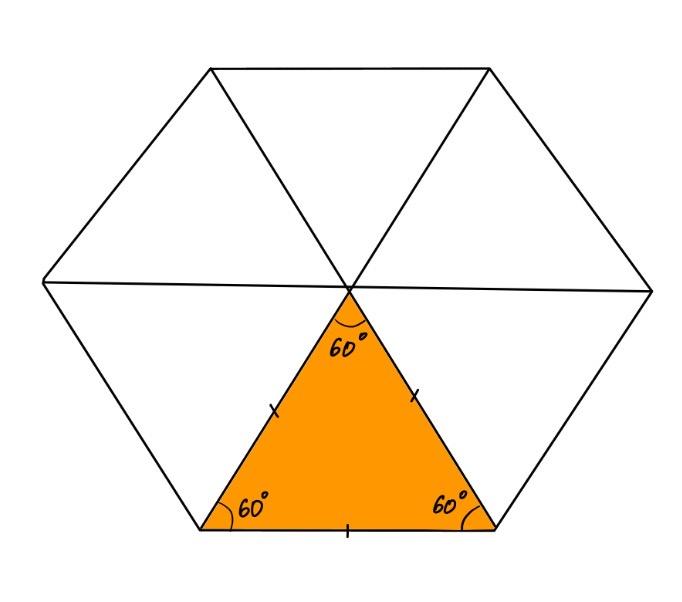
! Правильный шестиугольник — многоугольник с шестью равными сторонами и углами. Правильный шестиугольник состоит из шести правильных треугольников. Правильный треугольник = равносторонний треугольник. А в равностороннем треугольнике все углы равны 60 градусам.

Площадь и периметр

1. Периметр равен сумме длин всех его сторон.

P = 6a, где a — длина стороны шестиугольника

1. Для того, чтобы найти площадь правильного шестиугольника, необходимо найти площадь равностороннего треугольника и умножить её на шесть.

        S = 6 * (площадь треугольника)

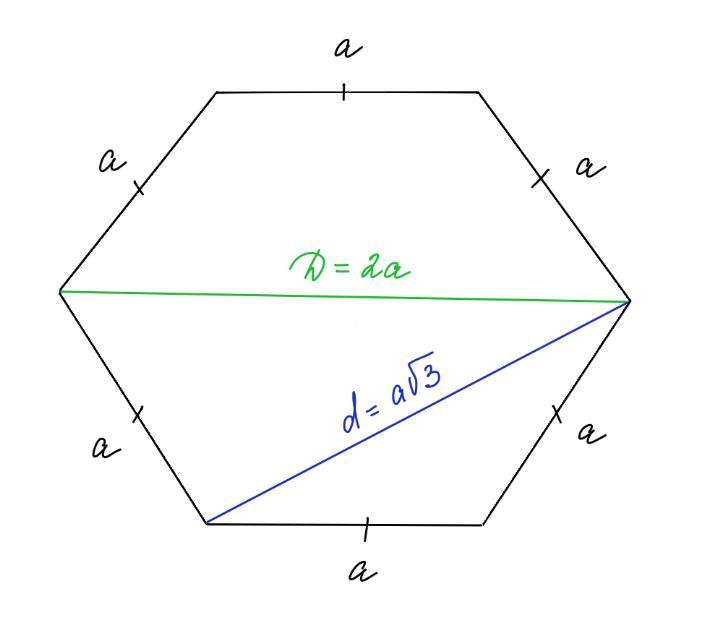
Диагональ правильного шестиугольника

Диагонали в правильном шестиугольнике бывают двух типов: малые (d) и большие (D).

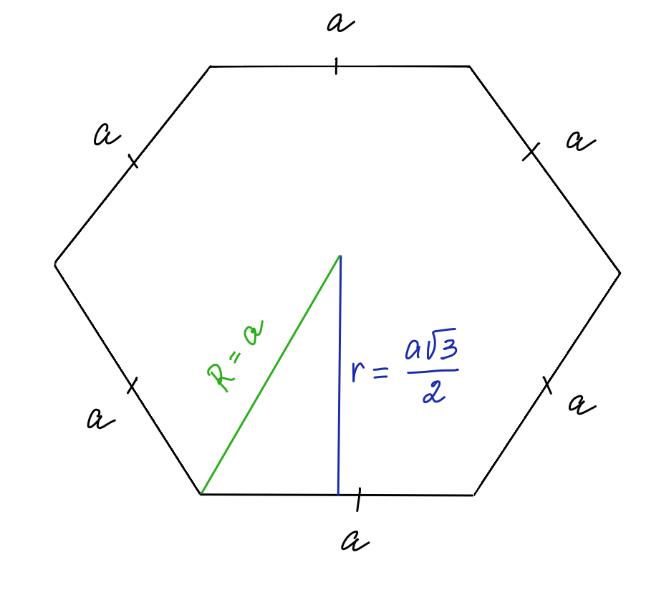
Радиусы вписанной и описанной окружностей

r — радиус вписанной окружности

R — радиус описанной окружности

! Обратите внимание на то, что радиусы окружностей в 2 раза меньше, чем диагонали.

Пример

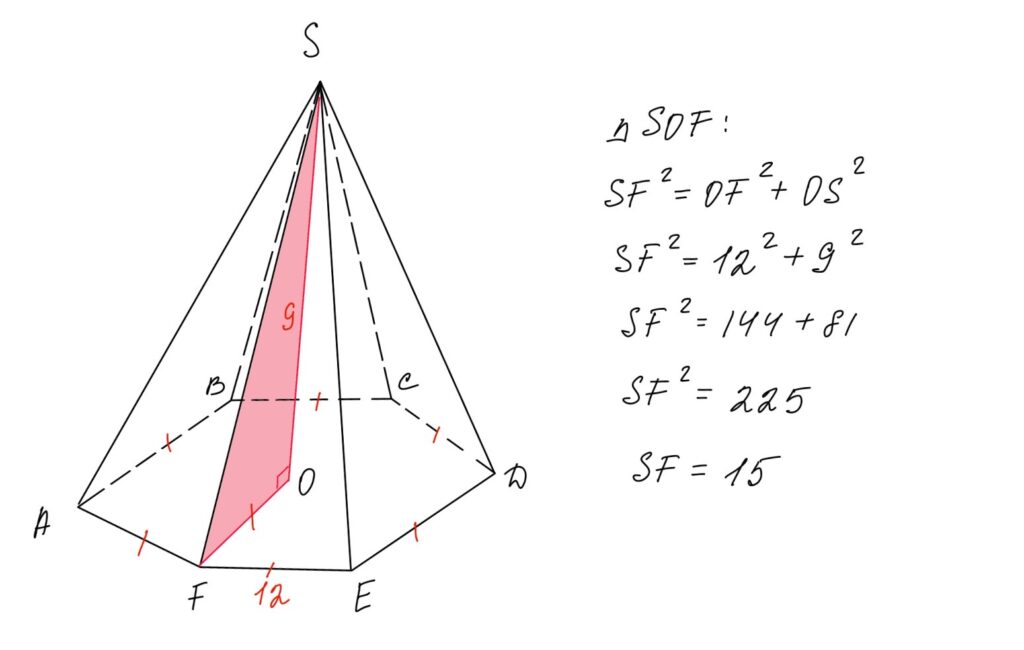
Стороны основания правильной шестиугольной пирамиды равны 12, высота равна 9. Найдите длину бокового ребра пирамиды.

Решение

1. Так как в основании лежит правильный шестиугольник, то он состоит из правильных треугольников, у которых все стороны равны FO = 12;
2. Рассмотрим треугольник SOF и найдём в нём по теореме Пифагора длину гипотенузы SF;
3. В правильных пирамидах все боковые рёбра равны SF = 15.

Ответ: 15