Планиметрия № 16
ЕГЭ профиль 2023

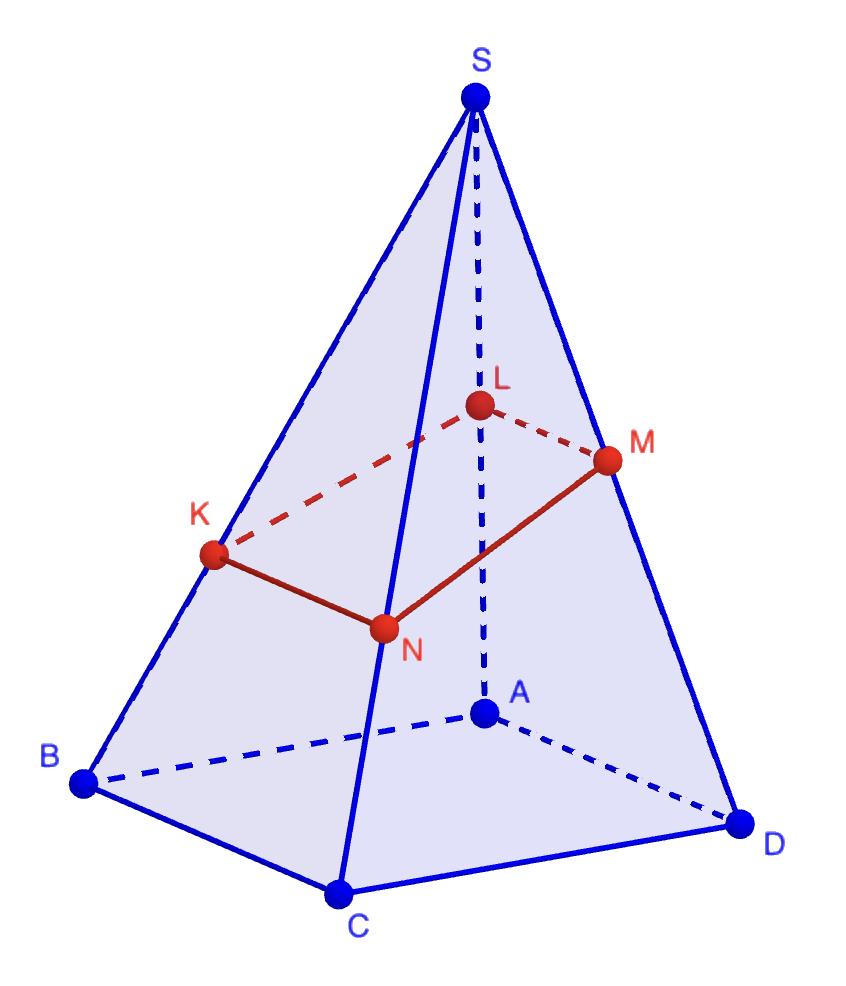
В основании четырёхугольной пирамиды SABCD лежит квадрат. Плоскость 𝛼 пересекает ребра SA, SB, SC, SD в точках L, K, M и N соответственно, причем SK : KB  3:1, а точки L и M – середины рёбер SA и SD.
а) Докажите, что четырёхугольник KLMN является трапецией, длины оснований которой относятся как 2:3.
б) Найдите высоту пирамиды, если угол между плоскостями ABC и  𝛼 равен 30°, площадь сечения пирамиды плоскостью 𝛼 равна 10√2 , а площадь основания пирамиды равна 32.

Решение:

Заметим, что LM – средняя линия в треугольнике SAD, следовательно, LM || AD. 

LM ∈ (KLM), LM || AD ⇒ AD || (KLM)

Так как AD || BC, то (KLM) || BC. 

Если плоскость проходит через прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна данной прямой.

BC ∈ (SBC), (KLM) ∩ (SBC) = KN ⇒ KN || BC. 

(KLMN) – искомое сечение.

LM || AD, KN || BC, BC || AD ⇒ LM || KN

KL ∦ NM ⇒ KLMN – трапеция.

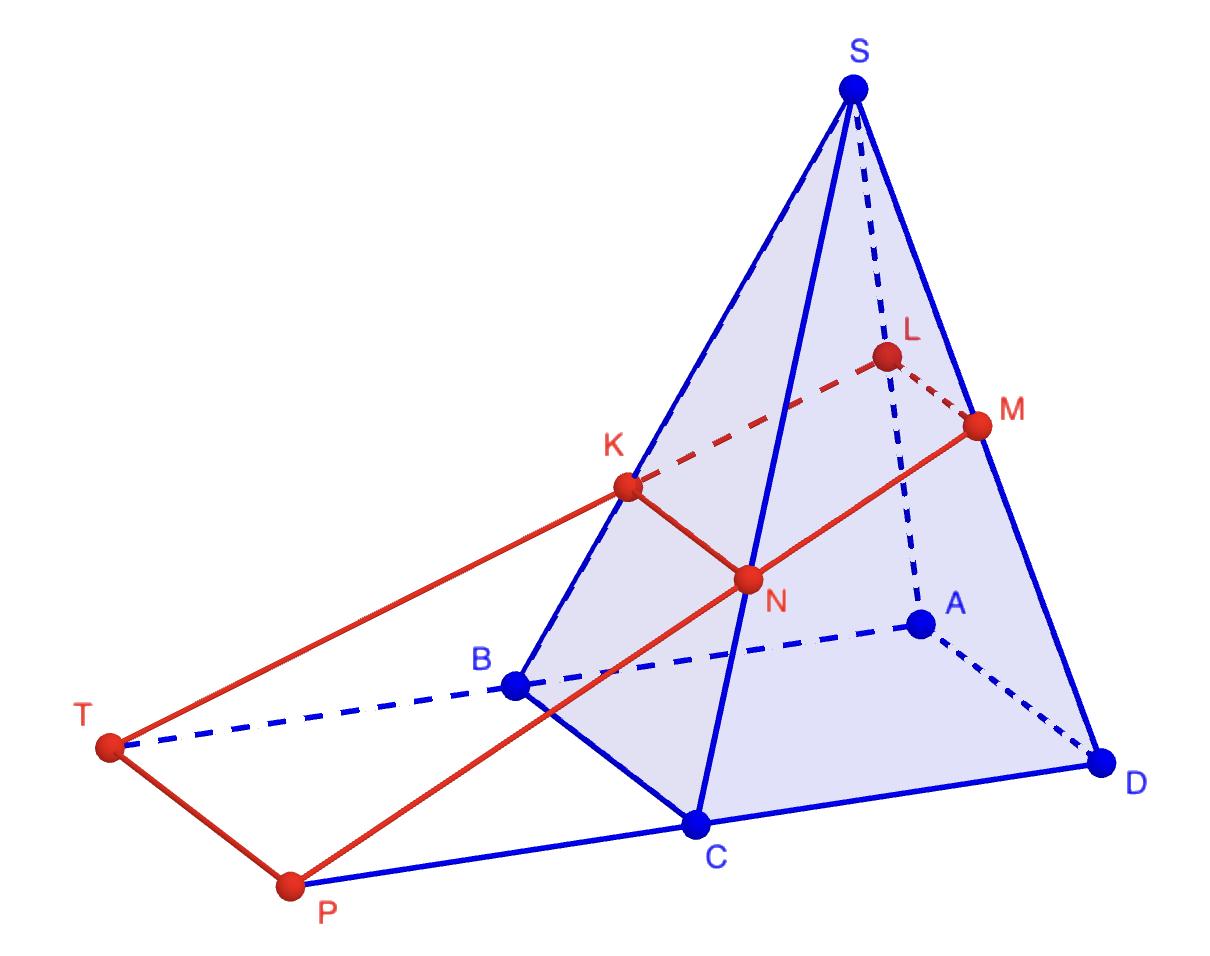
Пусть KL ∩ AB = T, а NM ∩ CD = P. 

Так как (KLM) ∩ (ABC) = TP, BC ∈ (ABC), (KLM) || BC, то TP || BC || AD || KN || LM.

Пусть AB = BC = CD = AD = a – сторона квадрата ABCD.

Так как LM – средняя линия, то LM = a/2.

∆SKN ~ ∆SBC (∠KSN – общий, ∠SKN = ∠SBC – как соответственные) ⇒ SK : SB = KN : BC = 3 : 4 ⇒ KN = 3a/4

Найдем отношение оснований трапеции KLMN: 

LM : KN = a/2 : 3a/4 = 2 : 3.  (ч.т.д.)

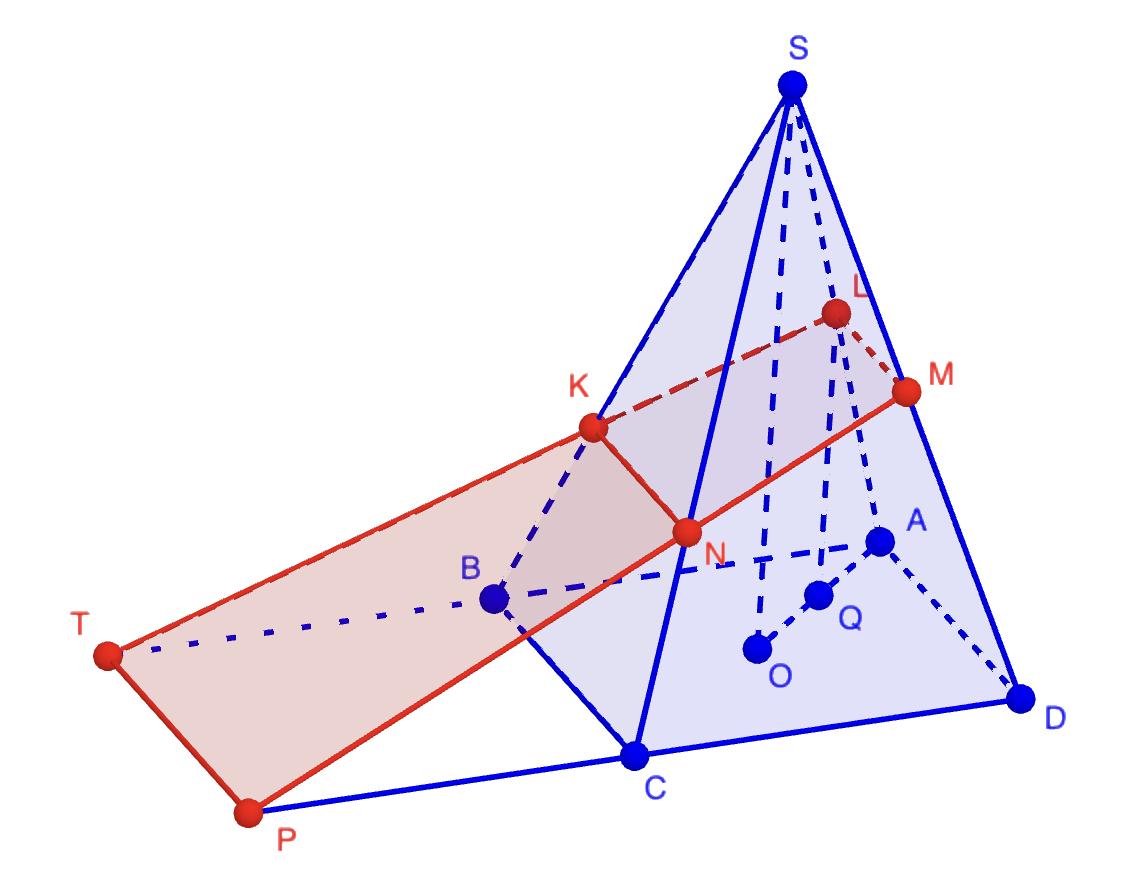
б) Пусть SO – высота пирамиды. Проведем LQ || SO. Так как SO ⟘ (ABC), то LQ ⟘ (ABC). Заметим, что LQ – средняя линия в ∆SOA, тогда SO = 2LQ.

По условию, a² = 32. Тогда a = 4√2.

LM = a/2 = 2√2.

KN = 3a/4 = 3√2.

TP = a = 4√2.

KN – средняя линия трапеции LMPT, так как KN = (LM+TP)/2.

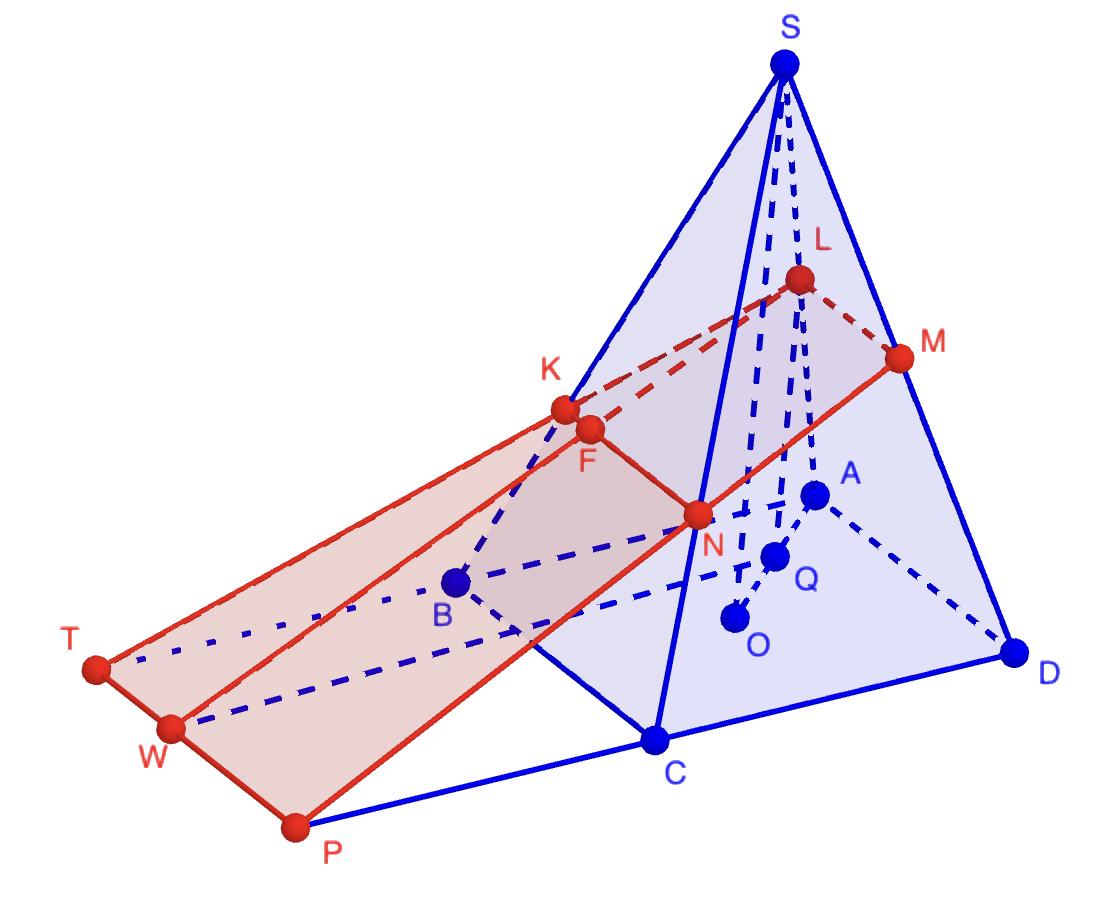
Пусть LW ⟘ TP и LW ∩ KN = F, тогда LF ⟘ KN и LF = LW/2.

(LM+KN)LF/2 = 10√2

(2√2+3√2)LF/2 = 10√2

5√2LF/2 = 10√2

LF = 4; LW = 2LF = 8.

QW – проекция LW на плоскость (ABC). LW ⟘ TP, тогда QW⟘TP по теореме о трех перпендикулярах.

LW⟘TP, LW ∈ (KLM), QW⟘TP, QW ∈ (ABC) ⇒ ∠LWQ = 30˚ как угол между плоскостями (KLM) и (ABC).

Тогда LQ = LW/2 = 4 как катет, лежащий напротив угла 30°.

Итого, SO = 2LQ = 8.

Ответ: 8