ЕГЭ профиль № 16
Остроугольный треугольник

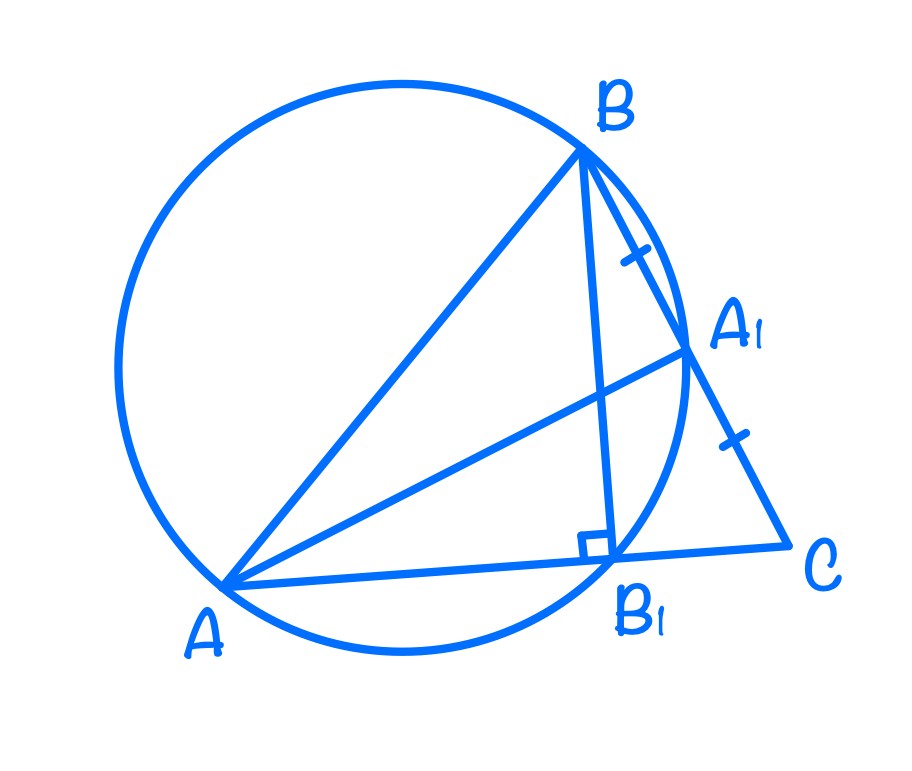
В остроугольном треугольнике ABC проведены высота BB₁ и медиана AA₁, причем точки A, B, B₁ и A₁ лежат на одной окружности.

а) Докажите, что треугольник АВС равнобедренный.

б) Найдите площадь треугольника ABC, если AA₁ : BB₁ = 4 : 3 и A₁B₁ = 3.

Решение:

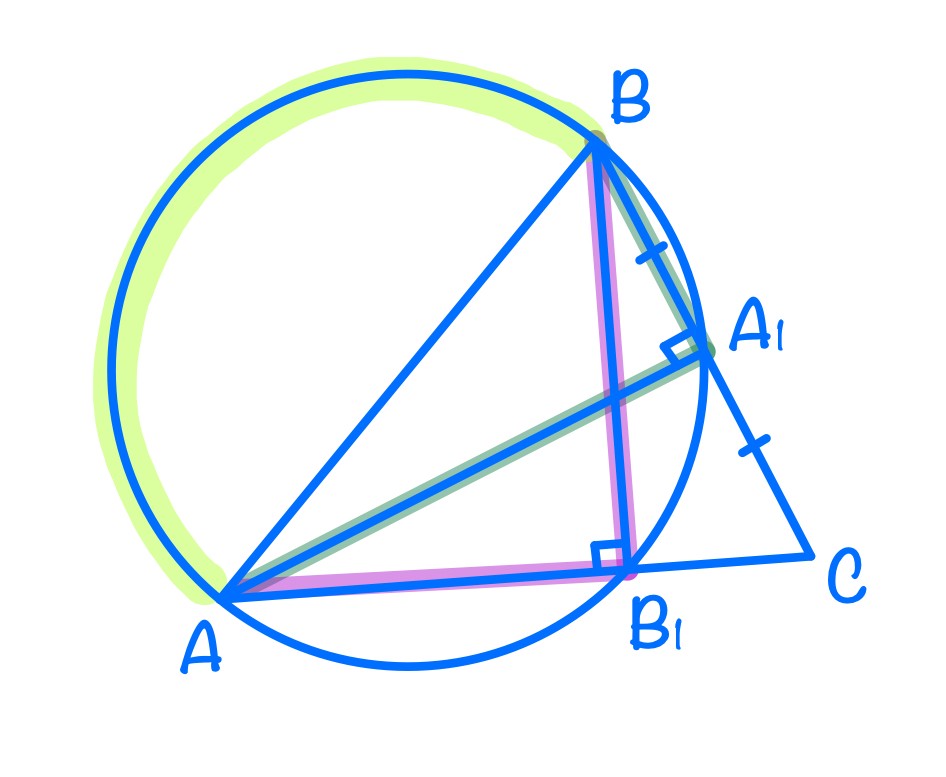
а) Углы AB₁B и AA₁B лежат на одной дуге, значит ∠AB₁B = ∠AA₁B = 90°.

Заметим, что в ∆ABC медиана AA₁ также является высотой, тогда ∆ABC — равнобедренный.

ч.т.д.

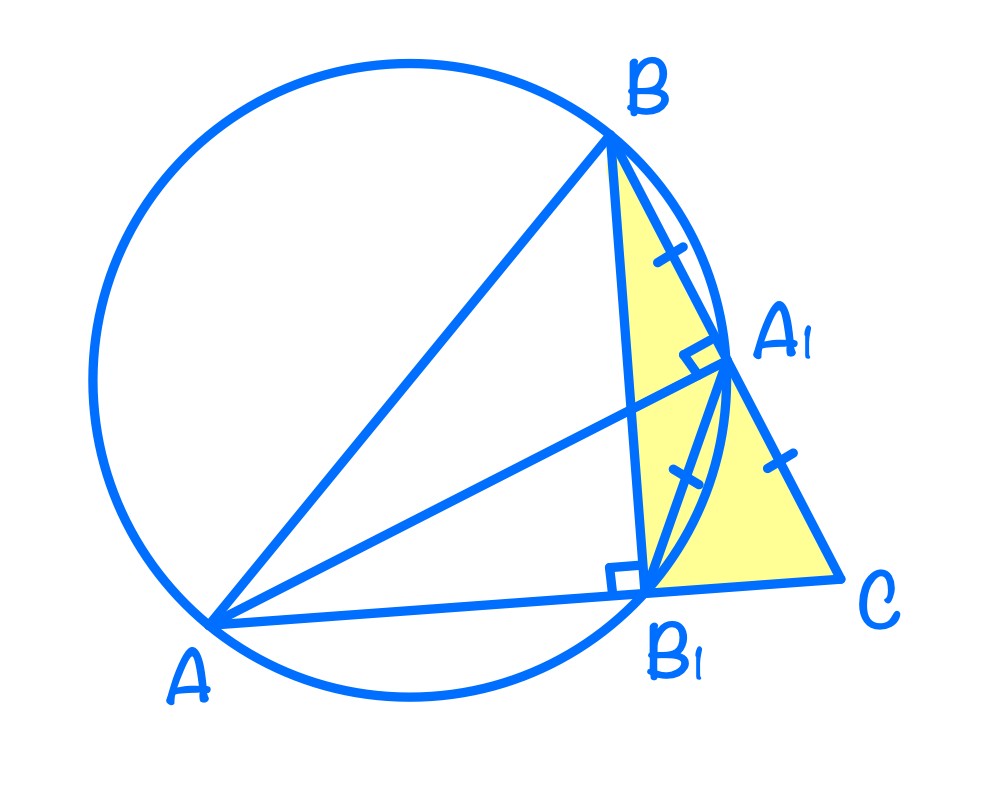
б) В ∆AB₁C из вершины прямого угла проведена медиана, значит, BA₁ = CA₁ = B₁A₁ = 3.

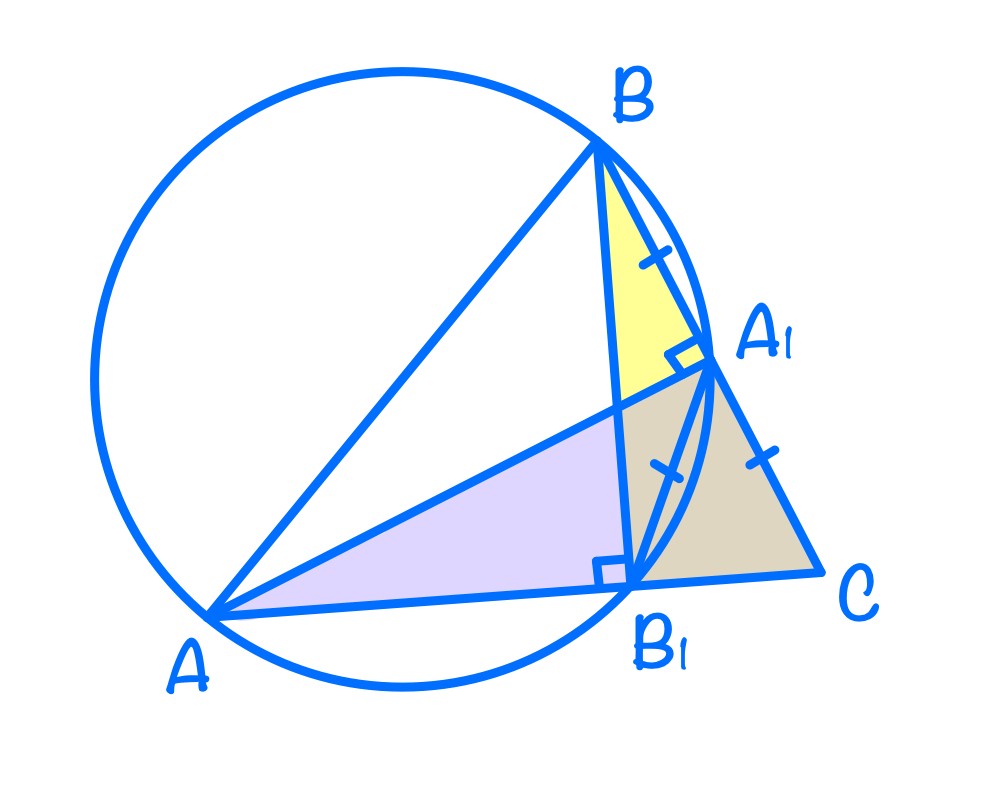
∆BB₁C ~ ∆AA₁C по двум углам (∠AA₁C = ∠BB₁C = 90°, ∠С — общий).

Тогда AA₁ : BB₁ = AC : BC = 4 : 3 .

Отсюда AC = 4/3 ∙ BC = 4/3 ∙ 6 = 8.

Рассмотрим теорему Пифагора для ∆AA₁C:

AA₁² = AB² — BA₁²

AA₁² = 8² — 3²

AA₁² = 64 — 9

AA₁² = 55

AA₁ = √55

Формула для нахождения площади треугольника ABC:

S = ½ ∙ AA₁ ∙ BC

Тогда S = ½ ∙ √55 ∙ 6 = 3√55.

Ответ: б) 3√55