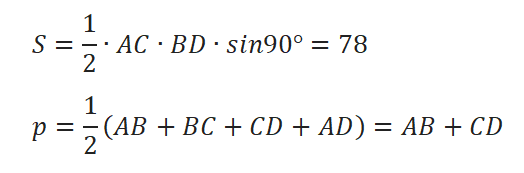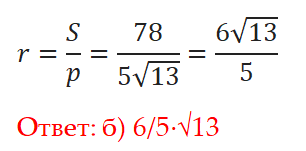ЕГЭ профиль № 16
Четырехугольник + окружности

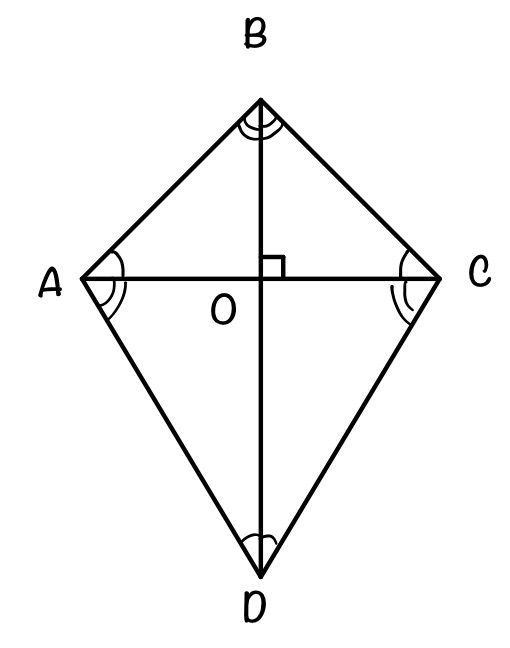
В четырехугольнике ABCD противоположные стороны не параллельны. Диагонали четырехугольника ABCD пересекаются в точке О под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин – точка О.

а) Докажите, что в четырехугольник ABCD можно вписать окружность.

б) Найдите радиус вписанной окружности, если AC = 12, BD = 13.

Решение:

а) Δ ABO = ΔCBO по катету и острому углу (BO – общая сторона, ∠ АВО = ∠ СВО  — по условию ) → АВ = СВ и АО = СО;

Δ ADO = ΔCDO по катету и острому углу (DO – общая сторона, ∠ АDО = ∠ СDО  — по условию ) → АD = СD и АО = СО;

Т.к. AB = CB и AD = CD, то AB + CD = CB + AD → в четырехугольник ABCD можно вписать окружность.

б) Т.к. АО = СО и АС = 12, то АО = СО = 6

Пусть BO = y, тогда DO = 13 — y

По свойству пересекающихся хорд AO ⋅ CO = BO ⋅ DO:

6 ⋅ 6 = у ⋅ (13-у)

у = 4 или у = 9

Если у = 4, то ВО = 4 и DO = 9

Если у = 9, то BO = 9 и DO = 4

Если в четырехугольник можно вписать окружность, то его площадь равна S = pr, где p – полупериметр четырехугольника, S – площадь четырехугольника, r – радиус вписанной окружности.

Площадь и полупериметр четырехугольника ABCD через диагонали и угол между ними:

Δ ABO: AB² = AO² + BO² = 6² + 9² = 117 → AB = √117 = 3√13

Δ ADO: AD² = AO² + DO² = 6² + 4² = 52 → AD = √52 = 2√13

Тогда полупериметр p = AB+ CD = 3√13 + 2√13 = 5√13

Радиус вписанной окружности: