ЕГЭ профиль № 13
Конус

Радиус основания конуса равен 12,а высота конуса равна 5. 

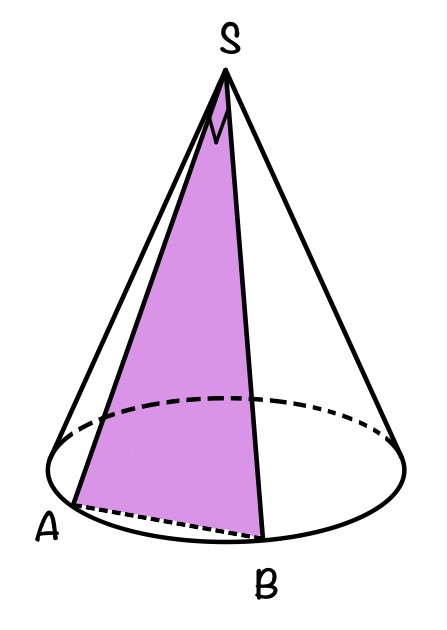
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. 

б) Найдите расстояние от плоскости сечения до центра основания конуса. 

Решение:

а) Пусть AS и BS – взаимно перпендикулярные образующие, т.е. AS⊥BS. Так как сечение проходит через взаимно перпендикулярные образующие и вершину конуса S, то сечение конуса плоскостью – треугольник △ASB. 

б) Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на плоскость. 

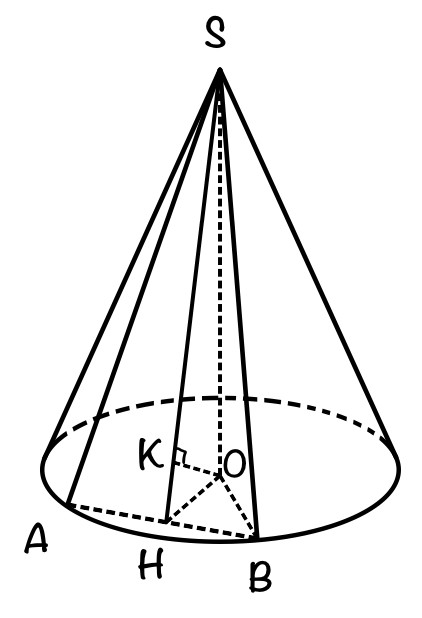
Образующие в конусе равны → AS = BS и△ASB  – равнобедренный. Тогда высота SH, проведённая из вершины прямого угла, также является биссектрисой и медианой, т.е. AH = BH. 

SH – наклонная, ОН – проекция наклонной. АВ⊥SH, тогда AB⊥OH (по теореме о трёх перпендикулярах). 

Проведём OK⊥SH → OK – расстояние от центра основания до плоскости сечения.  

△SOB: SB² = SO² + BO² = 25 + 144 = 169 → SB = 13

△ASB: AB² = AS² + BS² = 169 + 169 = 338 → AB = 13√2 и AH = BH = (13√2)/2

△SHB: SH² = SB² – HB² = 169 – 169/2 = 169/2 → SH = (13√2)/2

△OHB: OH² = OB² – HB² = 144 – 169/2 = 119/2 → OH = (√119)/(√2)

△OHS: OH·OS = OK·SH 

OK = (OH·OS)/SH = (√119·5·2)/(√2·13·√2) = (5√119)/13

Ответ: OK = (5√119)/13