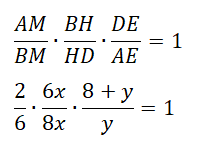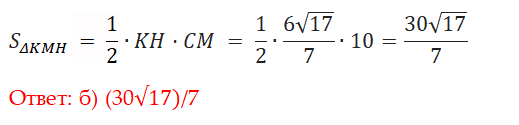ЕГЭ профиль № 13
Правильная четырехугольная пирамида

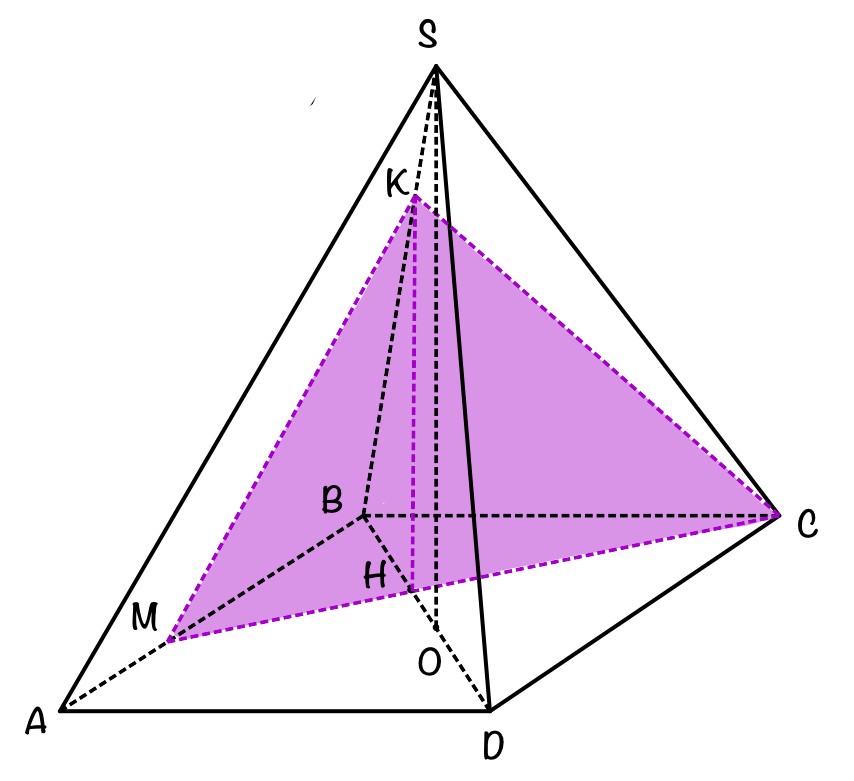
В правильной четырехугольной пирамиде SABCD сторона AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причем АМ = 2, SK = 1. Плоскость α перпендикулярна плоскости ABC и содержит точки M и K.

а) Докажите, что плоскость α содержит точку С.

б) Найдите площадь сечения пирамиды SABCD плоскостью α.

Решение:

а) SO – высота пирамиды SABCD. Опустим из точки K перпендикуляр KH на плоскость ABCD и рассмотрим Δ KBH и Δ SBO.

Δ KBH ~ Δ SBO по двум углам (∠В – общий, ∠BKH=∠BSO (соответственные углы при KH || SO и секущей BS)). Значит, SK/KB = OH/HB → OH/HB = 1/6 = x/6x, где х – одна часть.

Точка О – центр основания, т.е. BO = DO = 7x.

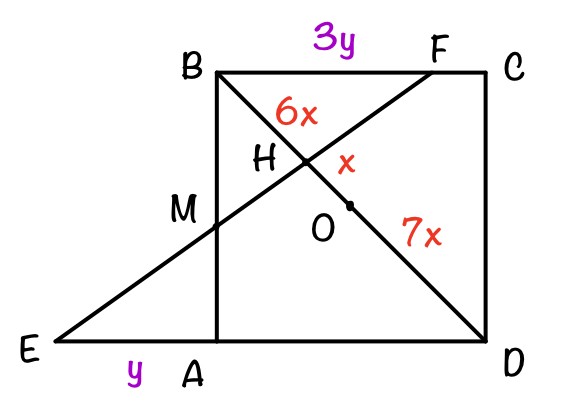
Пусть прямая MH пересекает сторону ВС в точке F, сторону AD — в точке E. Рассмотрим Δ МАЕ и Δ MBF.

Δ МАЕ ~ Δ MBF по двум углам (∠EMA = ∠FMB (как вертикальные), ∠MAE =∠MBF = 90°) → AM/MB = EA/FB = 2/6 = 1/3 = y/3y, где у – одна часть.

Запишем теорему Менелая для ΔABD:

y = 8/3 → EA = y = 8/3 и BF = 3y = 8.

Но BC = 8 и BF = 8 → C = F → Плоскость α проходит через точку С.

б) Сечение пирамиды плоскостью α – ΔKMH.

Т.к. Δ KBH ~ Δ SBO, то KH = 6/7⋅SO

ΔSOB: SO² = SB² — OB² = 7² — (4√2)² = 17 → SO = √17 → KH = 6/7⋅√17

ΔCMB: CM² = BM² + BC² = 6² + 8² = 100 → CM = 10