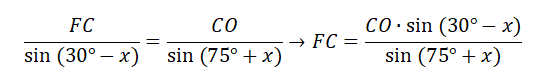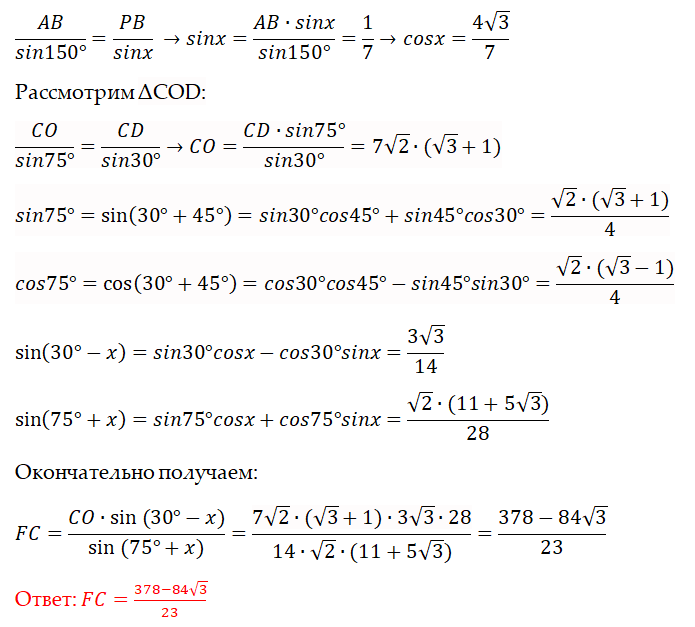ЕГЭ профиль № 16
Прямоугольник

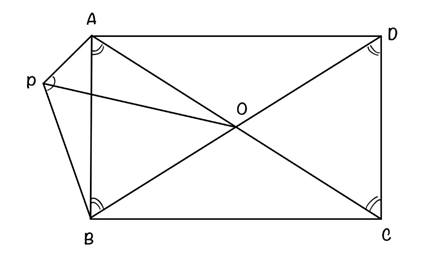
В прямоугольнике ABCD диагонали пересекаются в точке О, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°.

а) Докажите, что углыBAP и POB равны.

б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6√3 иBP=4.

Решение:

а) ∠DOC = 180° — ∠D — ∠C = 180° — 75° — 75° = 30°

∠DOC = ∠AOB = 30° (вертикальные углы)

∠PAB + ∠PBA = 180°-∠P=180°-150°=30°

∠PAO+∠PBO = ∠PAB+∠PBA+∠OAB+∠OBA = 30°+75°+75°=180°

∠APB+∠AOB = 150°+30°=180°

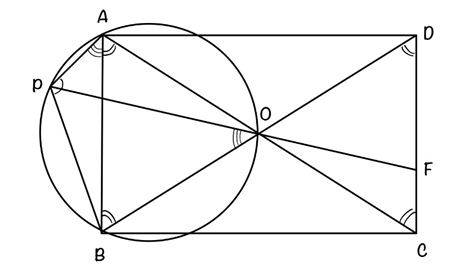
Сумма противоположных углов четырехугольника ABCD равна 180°, значит вокруг него можно описать окружность.

∠BAP и ∠POB опираются на дугу PB →∠BAP = ∠POB.

б) Пусть ∠BAP = ∠POB = х. Тогда ∠AOP = ∠COF = 30°-x.

В треугольнике ΔCOF∠CFO = 180°-∠FCO-∠COF = 180° — 75° — 30°+ x = 75°+ x

Тогда по теореме синусов для ΔCOF имеем:

Значит, необходимо найти sinx/cosx и сторону CO.

Теорема косинусов для ΔAPB:

AB²= AP² + PB² — 2⋅AP⋅PB⋅cos150° = 196 →AB = 14

Теорема синусов для ΔAPB: