ЕГЭ профиль № 16
Треугольник

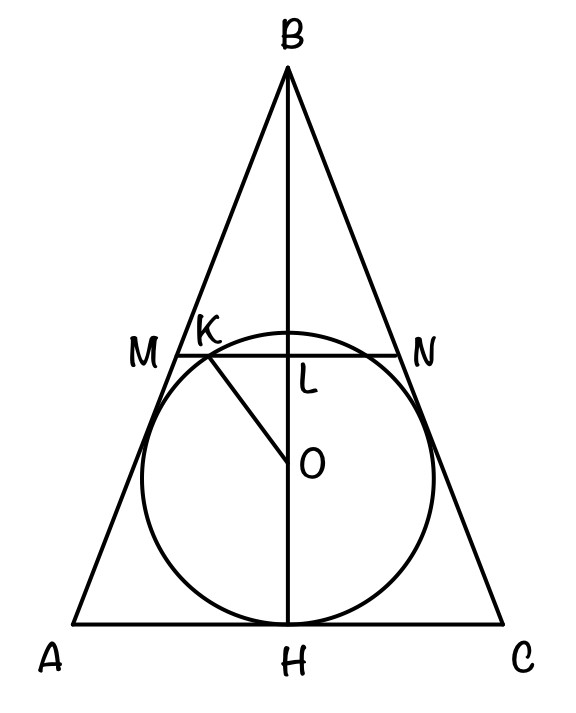
В треугольнике АВС известно, что АС = 26 и АВ = ВС = 38.

а) Докажите, что средняя линия треугольника, параллельная стороне АС, пересекает окружность, вписанную в треугольник АВС.

б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне АС.

Решение:

а)

Опустим высоту ВН на сторону АС, т.е. BH⟂AC

Так как MN – средняя линия, то MN || AC

→ MN ⟂ BH → △KLO – прямоугольный, тогда KO – гипотенуза и

KO > LO

Пусть r – радиус вписанной окружности, тогда KO = r и r > LO → MN пересекает окружность, вписанную в треугольник.

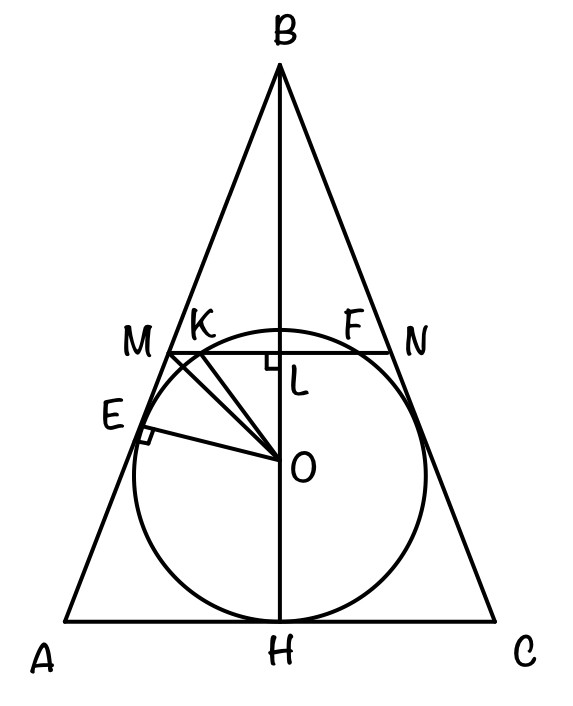
б)

Точка Е – точка касания вписанной окружности с боковой стороной △АВС. Тогда АЕ = АН = 13 ( если к окружности из одной точки проведены две касательные, то длины отрезков касательных от этой точки до точек касания с окружностью равны).

AM = BM = 38/2 = 19 (т.к. MN – средняя линия)

EM = AM – AE = 19 – 13 = 6

r = EO = HO = KO

△EMO: MO² = EM² + EO²

△MLO: LO² = MO² – ML²

△KLO: KL² = KO² – LO² = KO² – (MO² – ML²) = KO² – MO² + ML² = KO² – (EM²+EO²) + ML² = KO² – EM² – EO² + ML² = r² – 6² – r² + (13/2)² = 169/4 – 36 = 25/4 → KL = 5/2

Аналогично LF = 5/2

Тогда KF = KL + LF = 5/2 + 5/2 = 5

MK = ML – KL = 13/2 – 5/2 = 8/2 = 4

FN = LN – LF = 13/2 – 5/2 = 4

Получаем MK:KF:FN = 4:5:4

Ответ: б) 4:5:4