ЕГЭ профиль № 16
Сечение пирамиды

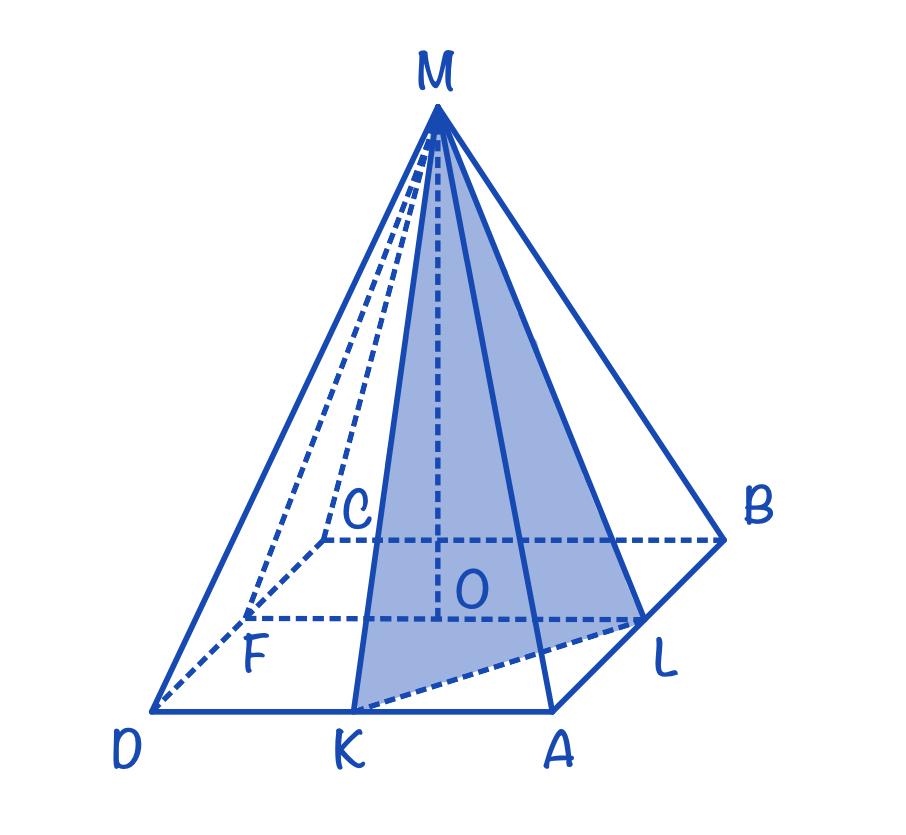
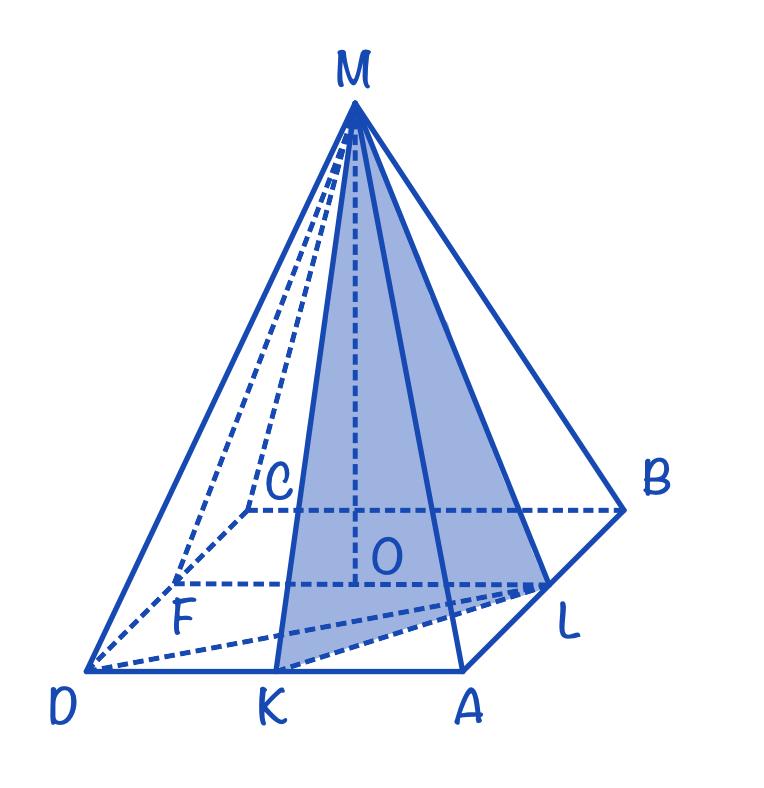
Противоположные боковые грани правильной четырехугольной пирамиды MABCD с основанием ABCD попарно перпендикулярны. Через середины K и L ребер AB и AD соответственно и точку М проведена плоскость α.

а) Докажите, что сечение пирамиды MABCD плоскостью α является равносторонним треугольником.

б) Найдите расстояние от точки D до плоскости α, если АВ = 9.

Решение:

а) Пусть F – середина CD

Так как противоположные боковые грани правильной четырехугольной пирамиды MABCD перпендикулярны, то MF⟂ML

Пирамида MABCD – правильная, значит проекция вершины M находится в центре основания (квадрата ABCD), то есть в точке О

Пусть AB = 2a, тогда AK = AL = a

△AKL: KL² = AK² + AL² = a² + a² = 2a² → KL = a√2

△MFL: MO⟂FL, MO – медиана, высота и биссектриса в равнобедренном треугольнике

Медиана, проведенная из вершины прямого угла равна половине гипотенузы. Отсюда получаем, что MO = FO = LO = a

△MOL: ML² = MO² + LO² = a² + a² = 2a² → ML = a√2

Боковые грани правильной пирамиды – равные равнобедренные треугольники. Так как треугольники равны, то равны и их медианы, то есть MF = ML = MK = a√2

Получаем, что KL = ML = MK = a√2 → △MKL – равносторонний треугольник → сечение пирамиды MABCD плоскостью α является равносторонним треугольником.

б) Расстояние от точки D до плоскости α является высотой пирамиды MDKL = ρ. Высоту пирамиды мы будем искать из объема пирамиды MDKL.

Рассмотрим пирамиду MABCD:

V_MABCD = 1/3⋅S_ABCD⋅h = 1/3⋅AB⋅AD⋅MO = 1/3⋅9⋅9⋅4,5 = 243/2

Рассмотрим пирамиду MDKL:

V_MDKL = 1/3⋅S_DKL⋅h

Пирамида MDKL имеет с пирамидой MABCD общую высоту h = MO = 4,5

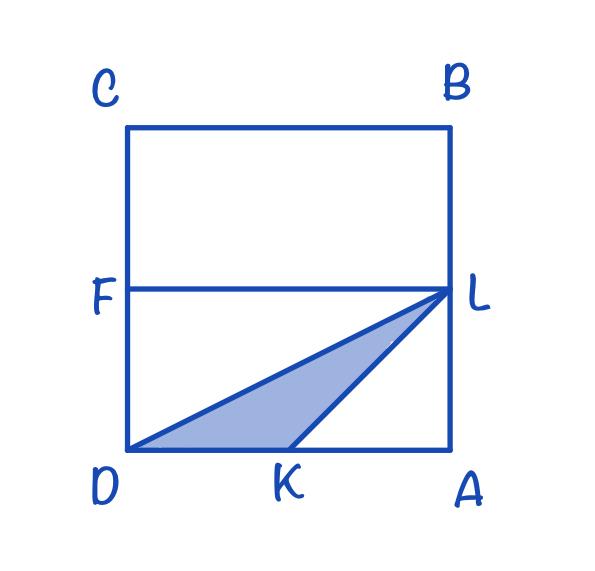
S_DKL = 1/2⋅S_DAL (медиана KL делит △DAL на два равновеликих треугольника) = 1/2⋅1/2⋅S_FDAL = 1/2⋅1/2⋅1/2⋅S_ABCD = 1/8⋅S_ABCD = 1/8⋅AB⋅AD = 1/8⋅81 = 81/8 = 10,125

Получаем V_MDKL = 1/3⋅S_DKL⋅h = 1/3⋅10,125⋅4,5 = 243/16

Запишем объем пирамиды MDKL через расстояние от точки D до плоскости α:

V_MDKL = 1/3⋅S_MKL⋅ρ

Найдем площадь треугольника MKL:

S_MKL = 1/2⋅KL⋅KM⋅sin60 = 1/2⋅(4,5√2) ⋅(4,5√2) ⋅(√3/2) = 10,125√3

Подставим известные значения в формулу V_MDKL = 1/3⋅S_MKL⋅ρ:

243/16 = 1/3⋅10,125√3⋅ρ

Найдем ρ:

ρ = 1,5√3

Ответ: б) 1,5√3