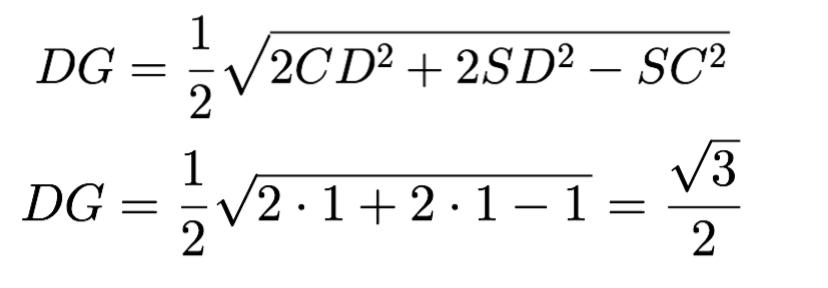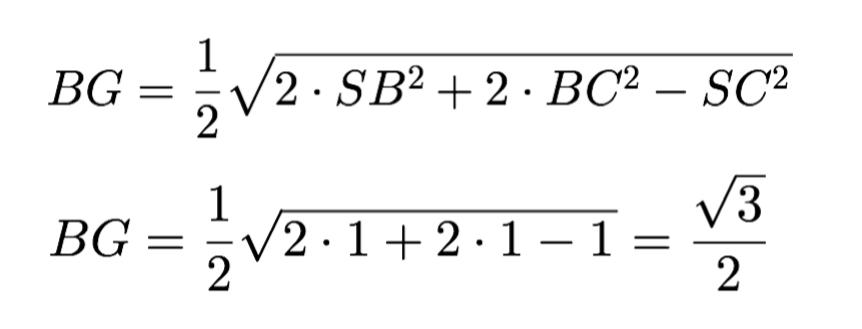Угол между плоскостями
ЕГЭ № 13

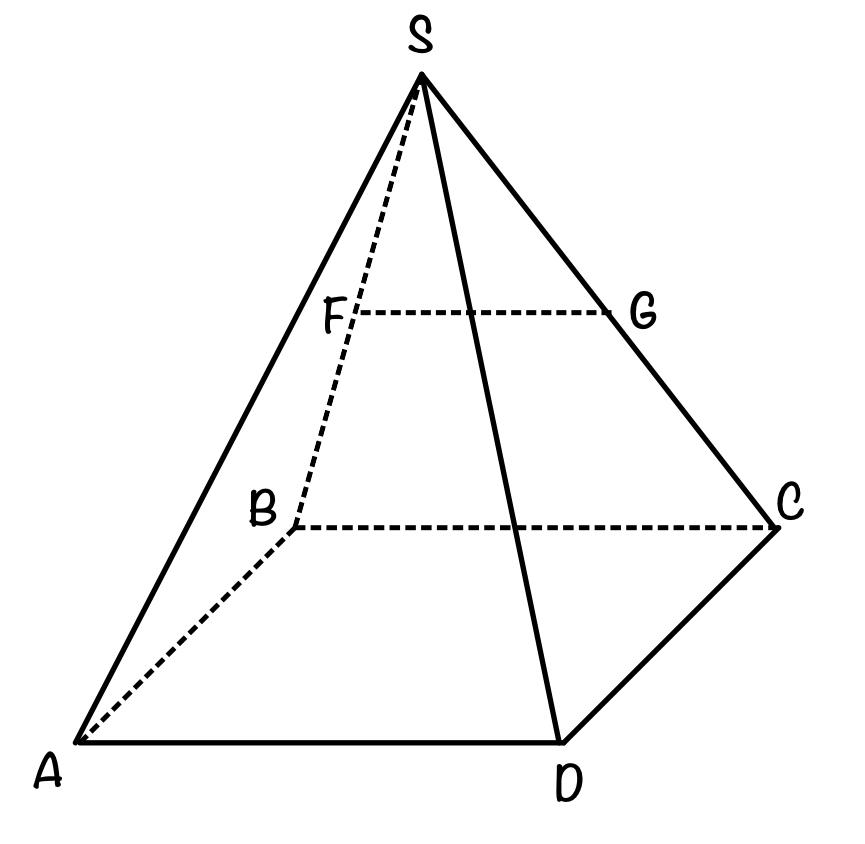
В правильной четырехугольной пирамиде SABCD все рёбра равны 1. Точка F – середина ребра SB, G – середина ребра SC.

а) Постройте прямую пересечения плоскостей ABG и GDF.

б) Найдите угол между плоскостями ABG и GDF.

Решение:

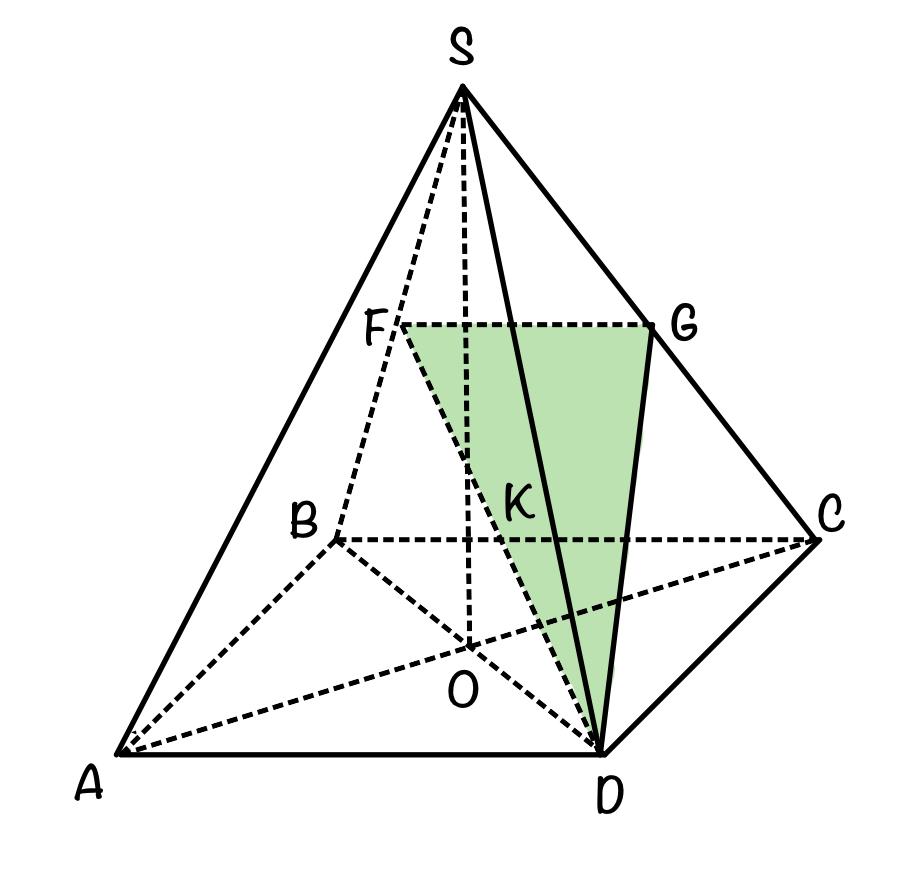
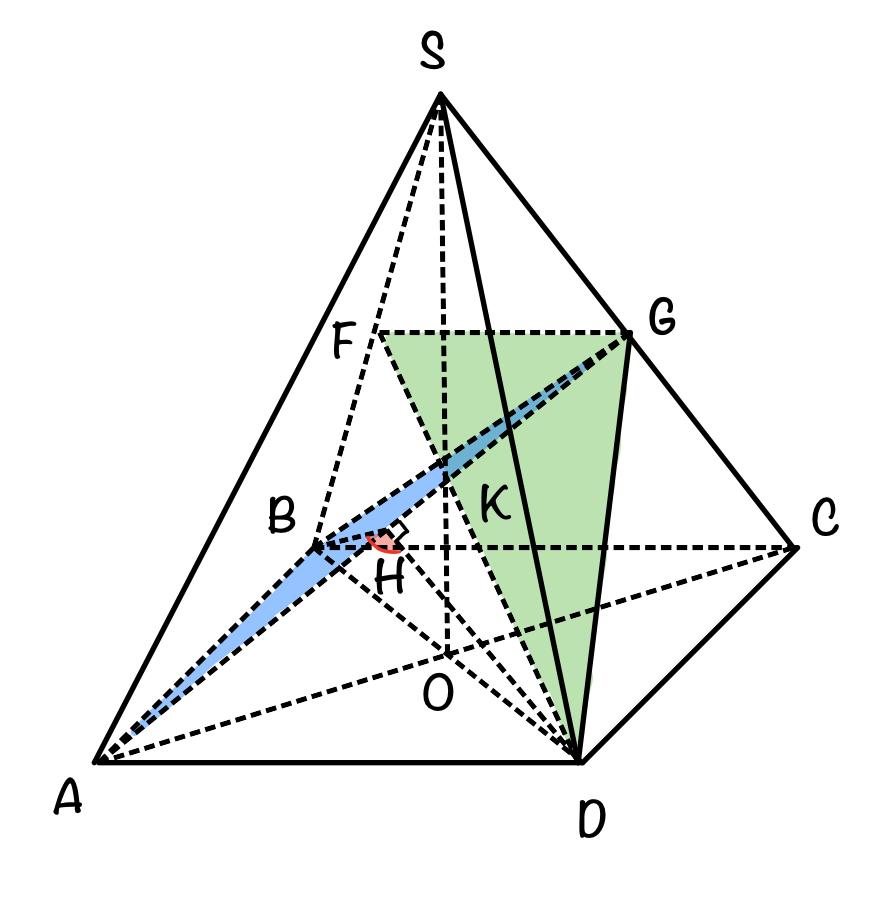
а) Проведём диагонали AC и BD, опустим высоту SO.

Соединим точки G, F и D.

SB = SD = 1 → △BSD – равнобедренный → BO = DO

BF = SF (по условию) → Точка К – точка пересечения медиан FD и SO → SK:KO = 2:1

Соединим точки A, B и G.

SA = SC = 1 → △ASC – равнобедренный → AO = CO

SG = CG (по условию) → Точка К – точка пересечения медиан AG и SO → SK:KO = 2:1

⬇

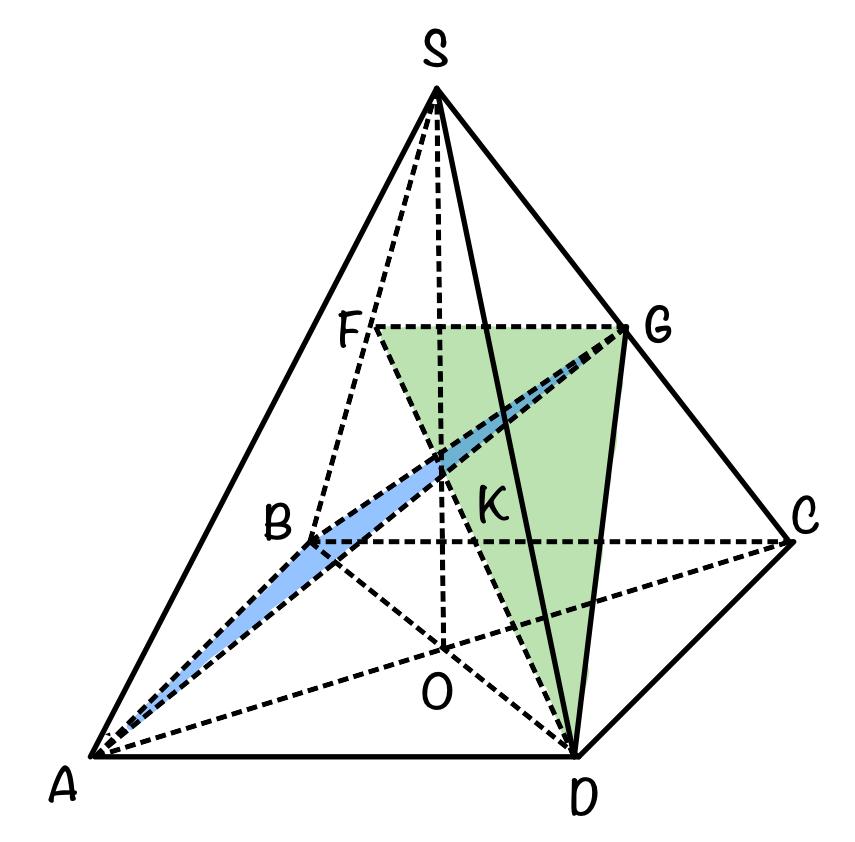
Плоскости ABG и GDF пересекаются в точках G и K

⬇

AG – прямая пересечения плоскостей ABG и GDF.

б) Угол между плоскостями – угол между перпендикулярами, проведёнными из этих плоскостей, к линии их пересечения.

△SCD (по свойству медианы):

△SBC (по свойству медианы):

△ABG = △ADG по трём сторонам (AG – общая, BG = DG = √3/2, AD = AB = 1)

Опустим перпендикуляр из точки B на прямую AG.

Опустим перпендикуляр из точки D на прямую AG (DH⟂AG) и рассмотрим △ADG:

GD² = AG² + AD² -2·AG·AD·cos∠GAD

3/4 = 5/4 + 1 – 2·(√5/2)·1·cos∠GAD

cos∠GAD = (3√5)/10

cos∠GAD = AH/AD

AH = AD·cos∠GAD =(3√5)/10

DH² = AD² – AH² = 1 – 45/100 = 55/100

DH = √55/10

Так как △ABG = △ADG, то DH = BH = √55/10

∠(ABG; GDF) = ∠BHD – угол между плоскостями ABG и GDF

Рассмотрим △BHD и напишем для него теорему косинусов:

BD² = BH² + DH² -2·BH·DH·cos∠BHD

(√2)² = (√55/10)² + (√55/10)² -2·(√55/10)·(√55/10)·cos∠BHD

2 = 55/100 + 55/100 -2·(55/100)·cos∠BHD

2 = 11/20 + 11/20 – 11/10·cos∠BHD

2 = 11/10 – 11/10·cos∠BHD

cos∠BHD = -9/11

∠BHD = arccos(-9/11) = π – arccos(9/11)

Ответ: б) π – arccos(9/11