Четырехугольник- параллелограмм Номер 16

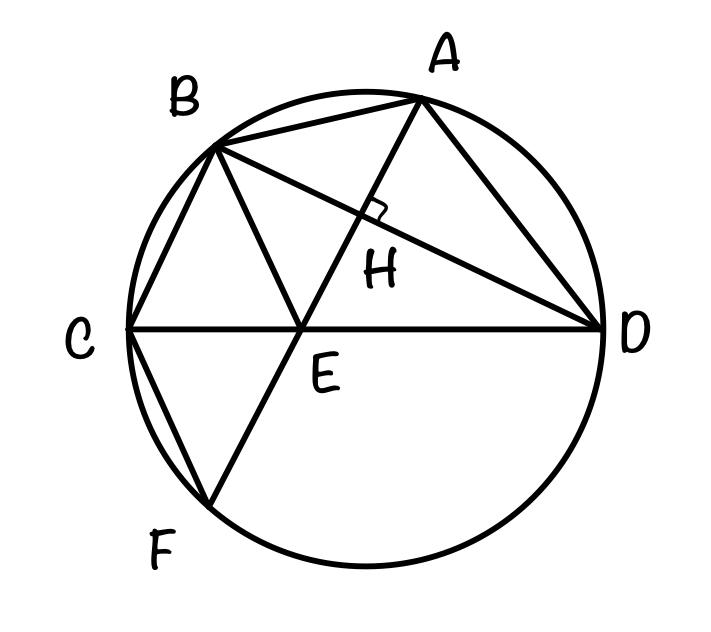
Четырёхугольник ABCD вписан в окружность, причем сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке Е, а окружность — в точке F, причем H — середина AE.

а) Докажите, что четырёхугольник BCFE — параллелограмм.

б) Найдите площадь четырёхугольника ABCD, если известно, что AB = 6 и AH = 2√5

Решение:

а) EH = AH, BH ⟂ AE → △ABE – равнобедренный → BE = AB →  ∠BAE = ∠BEA

Аналогично △ADE – равнобедренный → AD = ED →  ∠ADH = ∠EDH

Пусть ∠EDH = ∠ADH = х, тогда ◡BC = ◡AB = 2x (вписанный угол равен половине дуги, на которую он опирается)

∠CFA = 1/2◡ABC = 1/2(◡AB+◡BC) = 2x (вписанный угол)

∠CFA = ∠BEA = 2x (соответственные углы при секущей AF и прямых CF, BE)→ CF || BE

△CBD – прямоугольный треугольник → ∠BCD = 90-∠BDC = 90-x

△HED – прямоугольный треугольник→ ∠HED = 90-∠HDE = 90-x

∠HED = ∠BCD = 90-x (соответственные углы при секущей CD и прямых BC, AF) → BC || AF → BC || FE

Имеем:

BC || FE, CF || BE → BCFE – параллелограмм

б) △BHA: BH² = AB² – AH² = 36 – 20 = 16 → BH = 4

По свойству пересекающихся хорд имеем:

BH⋅DH = AH⋅FH

BH⋅DH = AH⋅(FE+EH)

(FE = CB, так как BCFE – параллелограмм)

4⋅DH = 2√5⋅(6 + 2√5)

4⋅DH = 20 + 12√5

DH = 5 + 3√5

S_ABED = 1/2⋅AE⋅BD = 1/2⋅4√5⋅(5 + 3√5 + 4) = 2√5⋅(9 + 3√5) = 30 + 18√5

S_BCFE = FE⋅BH = 6⋅4 = 24

S_CBE = 1/2⋅S_BCFE = 12

S_ABCD = S_CBE + S_ABED = 12 + 30 + 18√5 = 42 + 18√5

 Ответ: б) 42 + 18√5