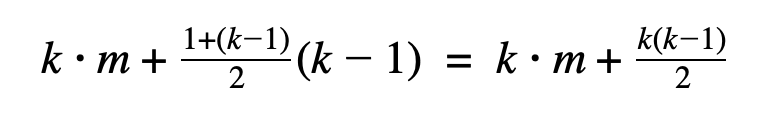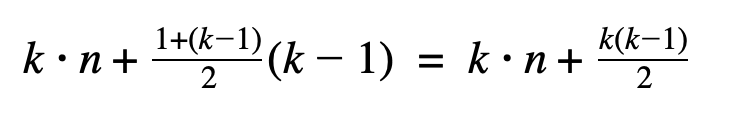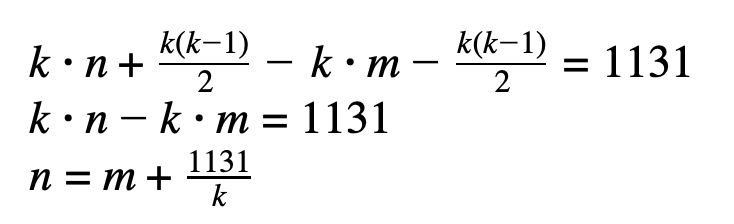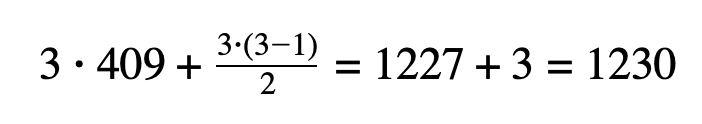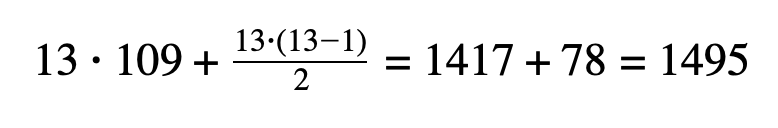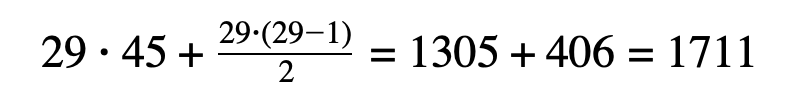ЕГЭ № 18 из сборника
«36 вариантов ФИПИ Ященко»

Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа – n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1131 фотографию больше, чем Маша, и что фотографировали они больше одного дня.

а) Могли ли они фотографироваться в течение 13 дней?

б) Могли ли они фотографироваться в течение 12 дней?

в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 35 фотографий?

Решение:

Так как m, n – число фотографий, сделанных Машей и Наташей в первый день, то m,n – целые числа.

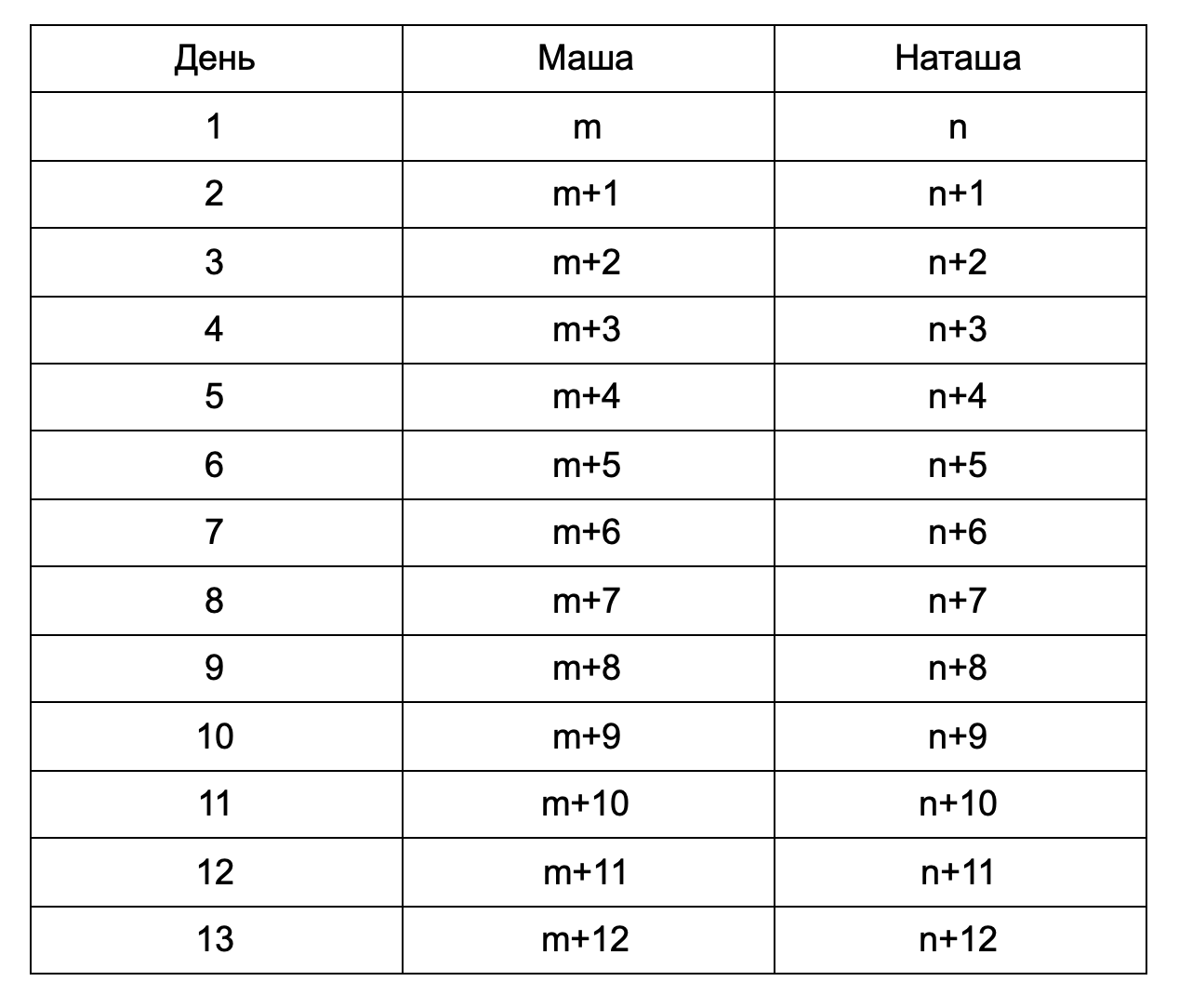
а) Распишем, сколько фотографий сделала каждая из девочек в течение 13 дней.

Тогда общее число фотографий, сделанных Машей, равно (13m+78).

Общее число фотографий, сделанных Наташей, равно (13n+78).

Известно, что Наташа за всё время сделала суммарно на 1131 фотографию больше, чем Маша, то есть (13n+78)-(13m+78)=1131

13n-13m=1131

n-m=87

n=m+87

Отсюда получаем, что девочки могли фотографироваться в течение 13 дней. Например, Маша в первый день сделала 1 фотографию, а Наташа (1+87)=88 фотографий.

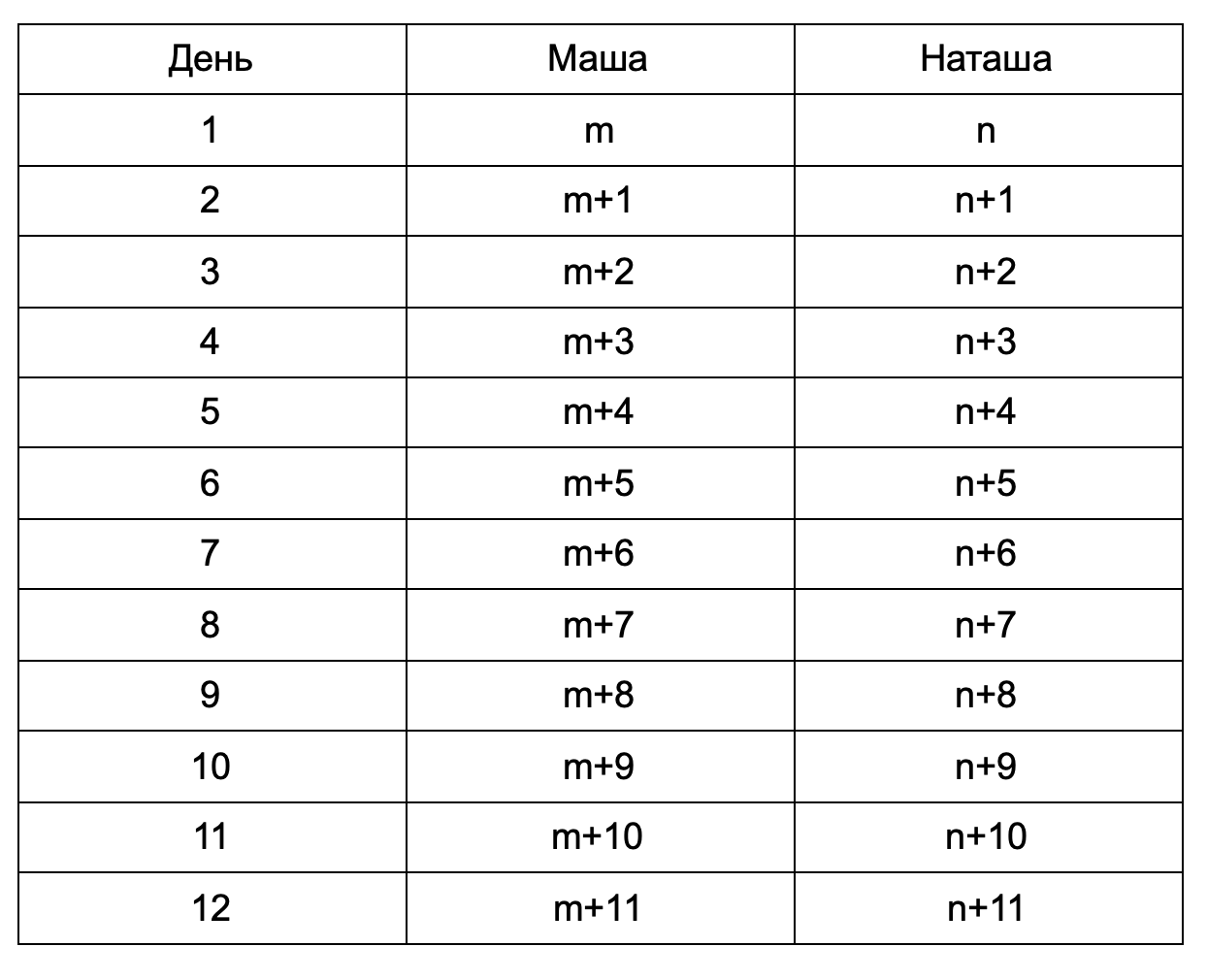
б) Распишем, сколько фотографий сделала каждая из девочек в течение 12 дней.

Тогда общее число фотографий, сделанных Машей, равно (12m+66).

Общее число фотографий, сделанных Наташей, равно (12n+66).

Известно, что Наташа за всё время сделала суммарно на 1131 фотографию больше, чем Маша, то есть (12n+66)-(12m+66)=1131

12n-12m=1131

4n-4m=377

n=m+377/4

Число 377 не делится нацело на 4, а числа m и n – целые, значит девочки не могли фотографироваться в течение 12 дней.

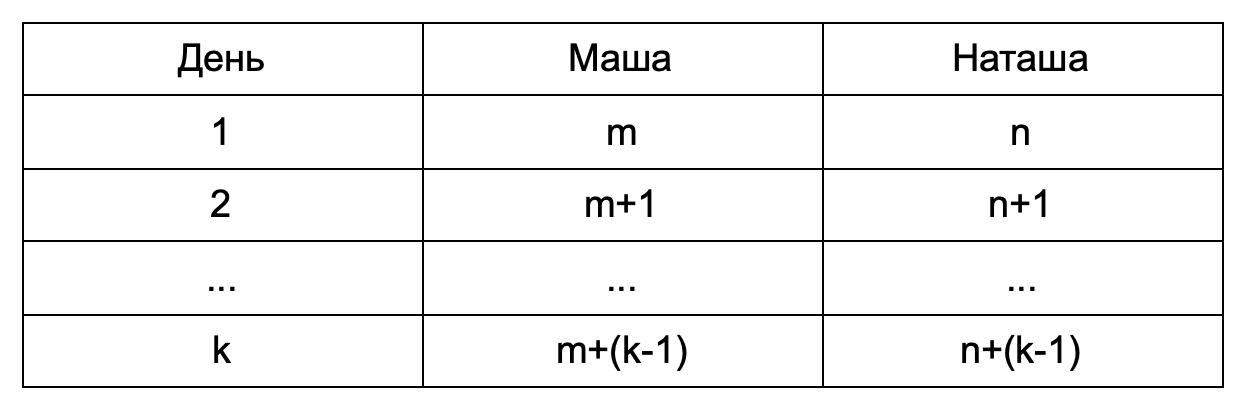
в) Распишем, сколько фотографий сделала каждая из девочек в течение k дней.

Тогда общее число фотографий, сделанных Машей, равно

Общее число фотографий, сделанных Наташей, равно

Известно, что в последний день Маша сделала меньше 35 фотографий, то есть m+k-1<35 или m+k<36

Известно, что Наташа за всё время сделала суммарно на 1131 фотографию больше, чем Маша, то есть

Отсюда получаем, что k – делитель числа 1131

Разложим число 1131 на множители: 1131 = 3⋅13⋅29

Пусть k = 3:

Тогда n = m+377 и m<33

Так как нам нужно, чтобы число фотографий было наибольшим, возьмем m=32, n=32+377=409 и найдем общее число фотографий, сделанных Наташей:

Пусть k = 13:

Тогда n = m+87 и m<23

Так как нам нужно, чтобы число фотографий было наибольшим, возьмем m=22, n=22+87=109 и найдем общее число фотографий, сделанных Наташей:

Пусть k = 29:

Тогда n = m+39 и m<7

Так как нам нужно, чтобы число фотографий было наибольшим, возьмем m=6, n=6+39=45 и найдем общее число фотографий, сделанных Наташей:

Получаем, что наибольшее суммарное число фотографий, которое могла сделать Наташа за все дни фотографирования, 1711.

Ответ: а) да; б) нет; в) 1711