ЕГЭ № 13 из сборника Ященко

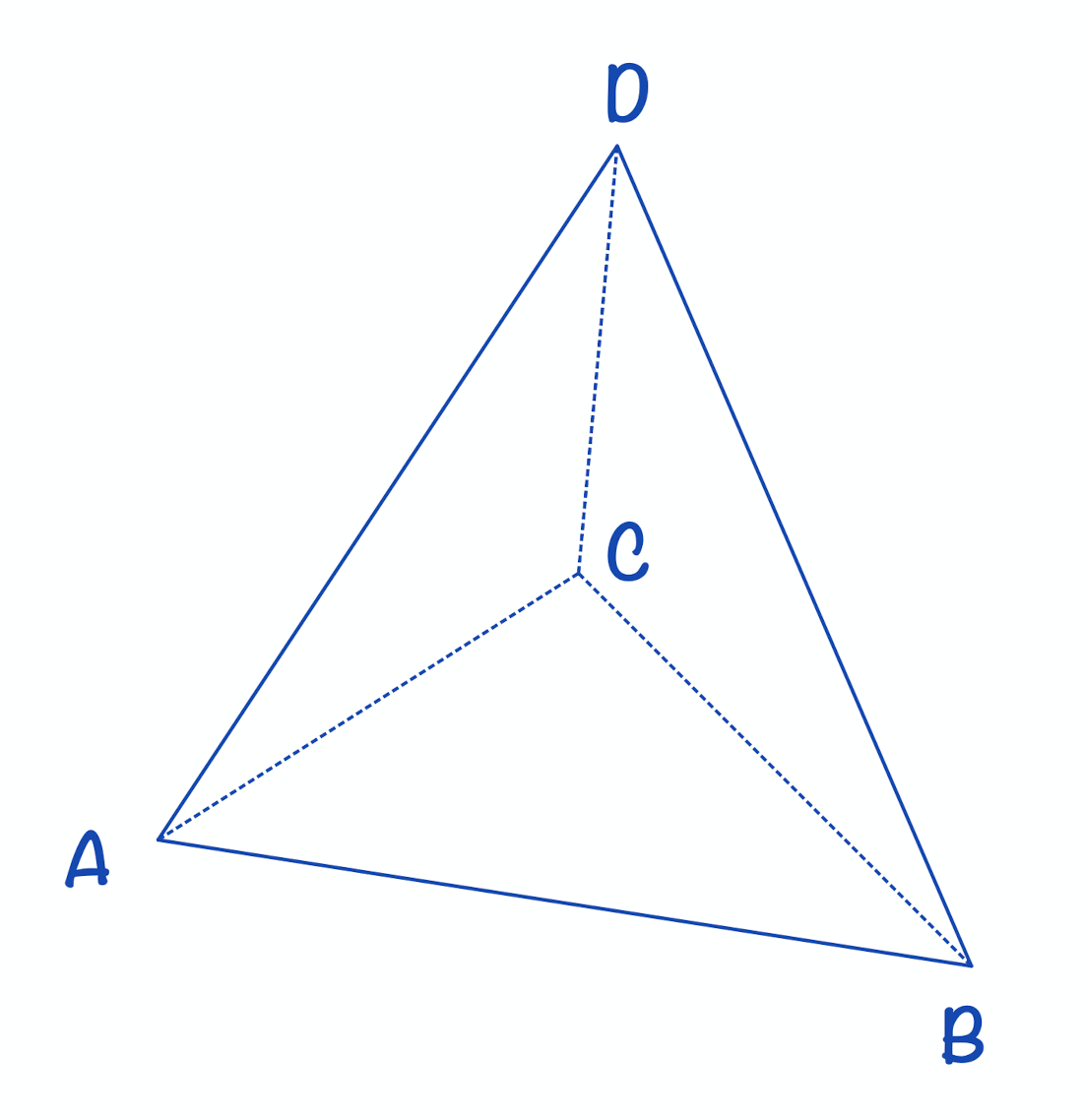
В пирамиде ABCD ребра DA, DB и DC попарно перпендикулярны, а AB = BC = AC = 10.

а) Докажите, что эта пирамида правильная.

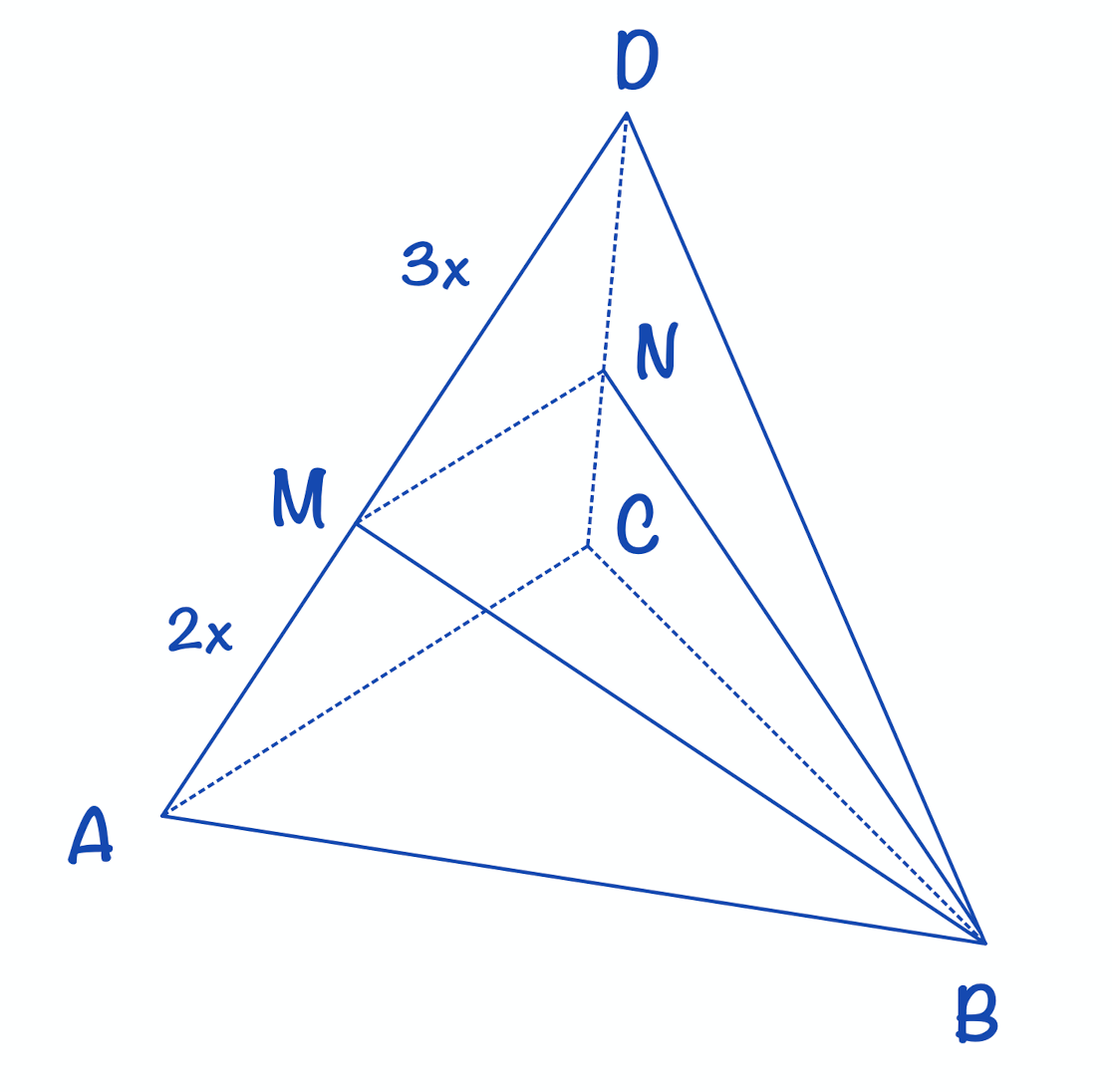
б) На ребрах DA и DC отмечены точки M и N соответственно, причем DM:MA = DN:NC = 3:2. Найдите площадь сечения MNB.

Решение:

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

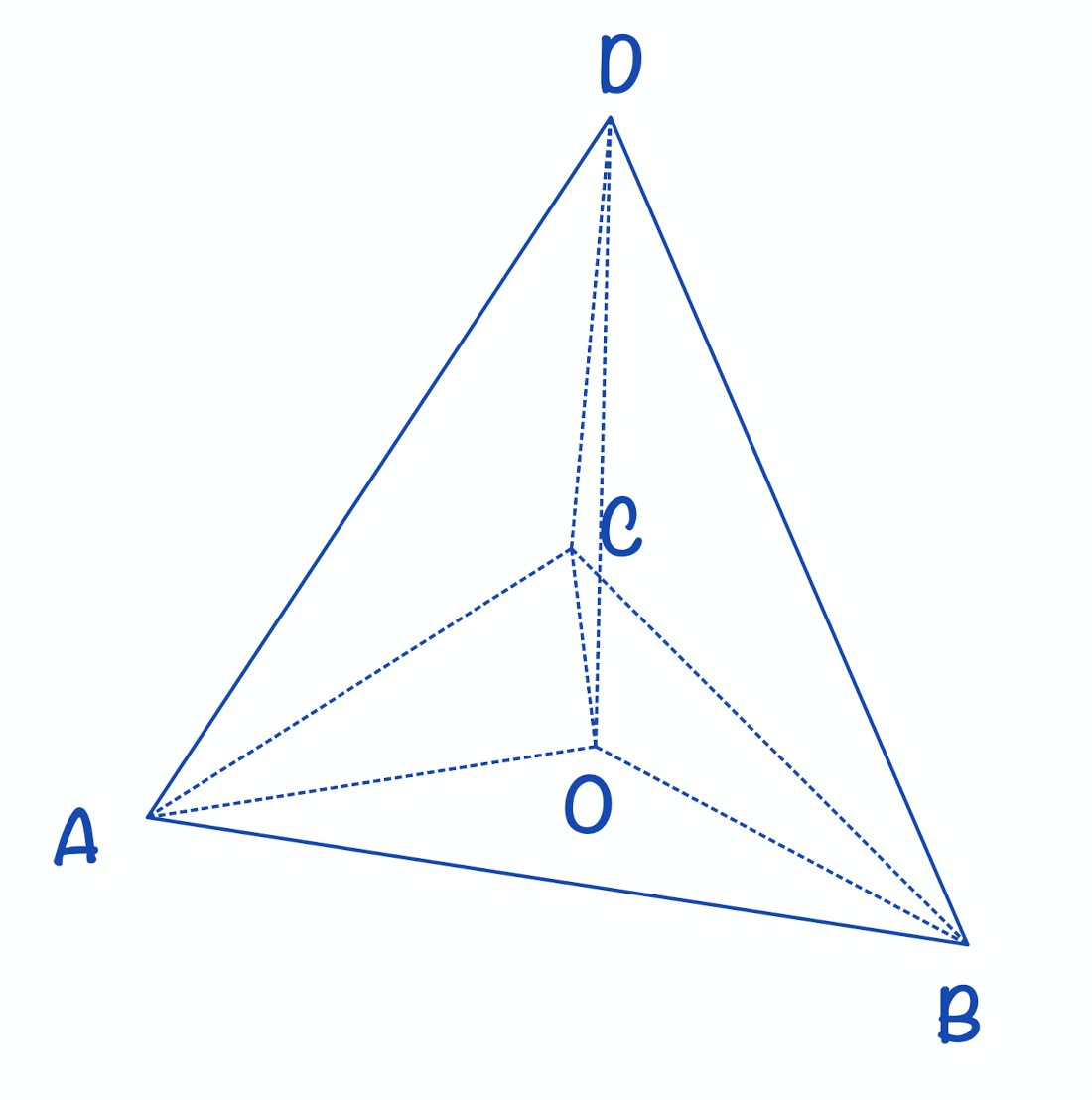
а) Проведем DO⟂(ABC).

AD⟂DB, AD⟂DC => AD⟂(DBC)=> AD⟂BC (т.к. ВС ∈ (DBC))

DO⟂(ABC) => DO⟂BC (т.к. ВС ∈ (ABC) )

Т.к. DO⟂BC и AD⟂BC => BC⟂(ADO) => BC⟂AO (AO ∈ (ADO))

Аналогично BC⟂СO, BC⟂ВO. Тогда О – точка пересечения высот ∆АВС, т.е. О – центр ∆АВС и DABC – правильная пирамида.

б)

∆DMN~∆DAC (∠D – общий, DM:DA = DN:DC = 3:5 ) по углу и двум пропорциональным сторонам =>

MN/AC = DM/DA

MN/10 = 3/5

MN = 6

Т.к. DABC – правильная пирамида, то DA = DB = DC = 5x. Рассмотрим ∆DAB =>

AB² = AD² + BD²

10² = (5x)² + (5x)²

100 = 50x²

x² = 2

x = √2

Получаем, что DA = DB = DC =5√2, AM = 2√2, MD = 3√2.

∆ADB – равнобедренный и прямоугольный, тогда ∠DAB = ∠DBA = 45˚.

∆AMB: MB² = AM² + AB² – 2⋅AM⋅AB⋅cos∠MAB

MB² = (2√2)² + 10² – 2⋅2√2⋅10⋅(√2/2)

MB² = 8 + 100 – 40

MB² = 68

MB = 2√17

Аналогично NB = 2√17

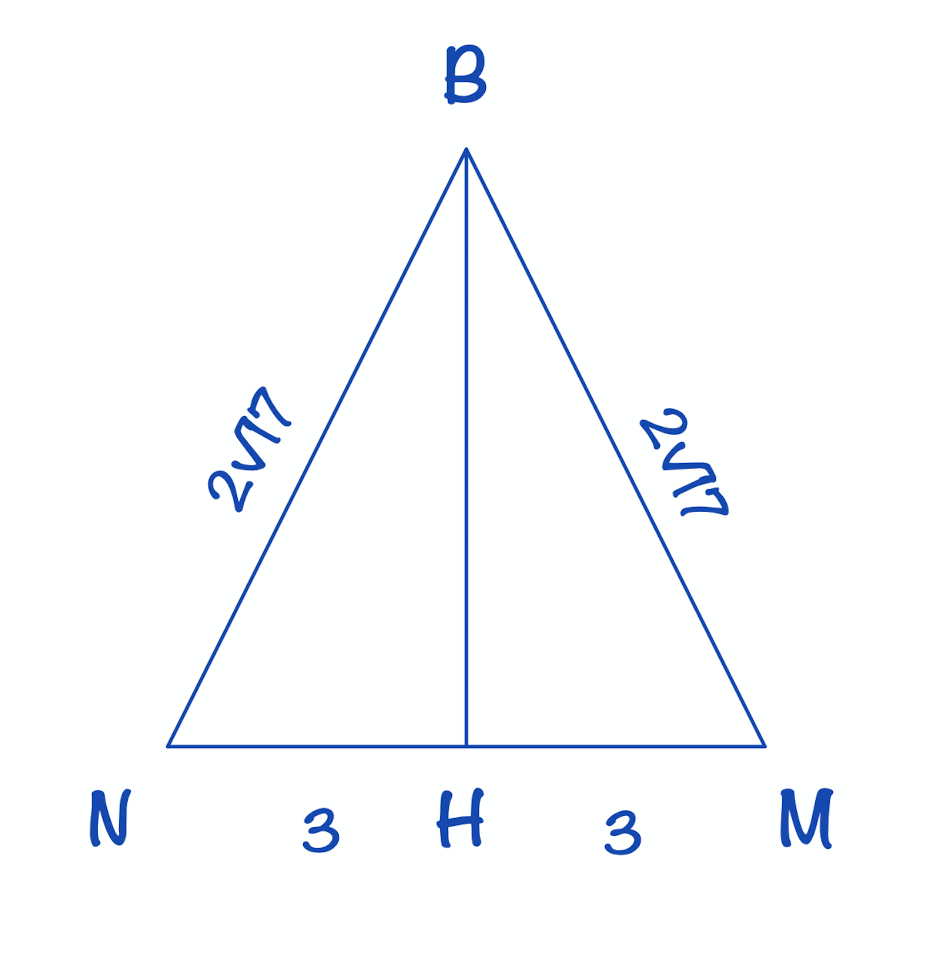
∆NBH: BH² = NB² – NH²

BH² = (2√17)² – 3²

BH² = 68 – 9

BH² = 59

BH = √59

S_MNB = 1/2⋅BH⋅NM = 1/2⋅√59⋅6 = 3√59

Ответ: б) 3√59