ЕГЭ № 3
Тангенс угла в треугольнике

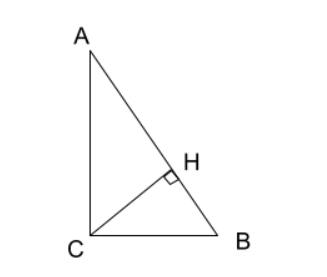
В треугольнике АВС угол С равен 90°, AB = 82, tgA = ⅘. Найдите высоту CH.

Решение:

Тангенс угла — это отношение противолежащего катета к прилежащему.

Рассмотрим ∆ABC:

tgA = BC/AC

tgA = ⅘

Тогда мы имеем следующее:

 ⅘ = BC/AC

Пусть x — одна часть, тогда BC = 4x, AC = 5x

Запишем теорему Пифагора для ∆ABC:

AC2 + BC2 = AB2 

(5x)2 + (4x)2 = 822 

25x2 + 16x2  = 822 

41x2  = 822 

x2  = 164

х = 2√41

Получаем:

BC = 4x = 8√41

AC = 5x = 10√41

Высота, опущенная на гипотенузу, выражается через стороны по формуле:

CH = (AC ⋅ BC)/AB

CH = (10⋅41⋅8)/82

CH = 40

Ответ: 40