Тангенс угла
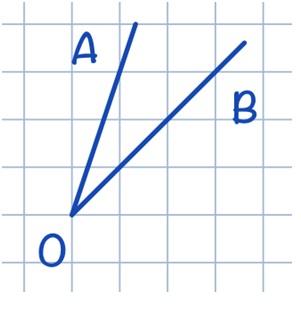
На клетчатой бумаге с размером клетки 1х1 изображен угол АОВ. Найдите тангенс этого угла.
Решение:
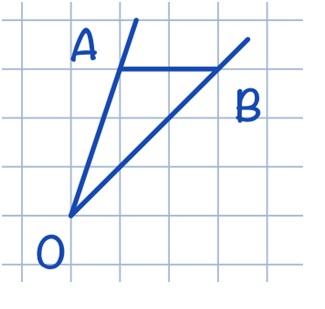
Достроим ∠AOB до треугольника ∆AOВ:
Найдем стороны ∆AOB:
AB = 2
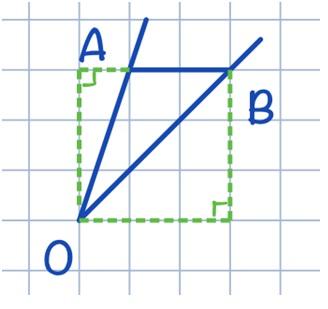
AO² = 3² + 1² = 9 + 1 = 10 => AO = √10
OB² = 3² + 3² = 9 + 9 = 18 => OB = √18
Запишем теорему косинусов для ∆AOB:
AB² = AO² + OB² – 2⋅AO⋅OB⋅cos∠AOB
2² = √10² + √18² – 2⋅√10⋅√18⋅cos∠AOB
4 = 10 + 18 – 2⋅√180⋅cos∠AOB
2⋅√180⋅cos∠AOB = 24
cos∠AOB = 12/√180
Найдем sin∠AOB из основного тригонометрического тождества:
sin²∠AOB + cos²∠AOB = 1
sin²∠AOB = 1 – cos²∠AOB
sin²∠AOB = 1 – (12/√180)²
sin²∠AOB = 1 – 144/180
sin²∠AOB = 36/180
sin∠AOB = 6/√180
Тогда tg∠AOB = sin∠AOB/cos∠AOB
tg∠AOB = (6/√180)/(12/√180) = 6/12 = 0,5
Ответ: 0,5

Привет ! Меня зовут Надежда. Я автор и ведущая курсов подготовки к ОГЭ и ЕГЭ по математике.