Задача в координатах. Площадь трапеции

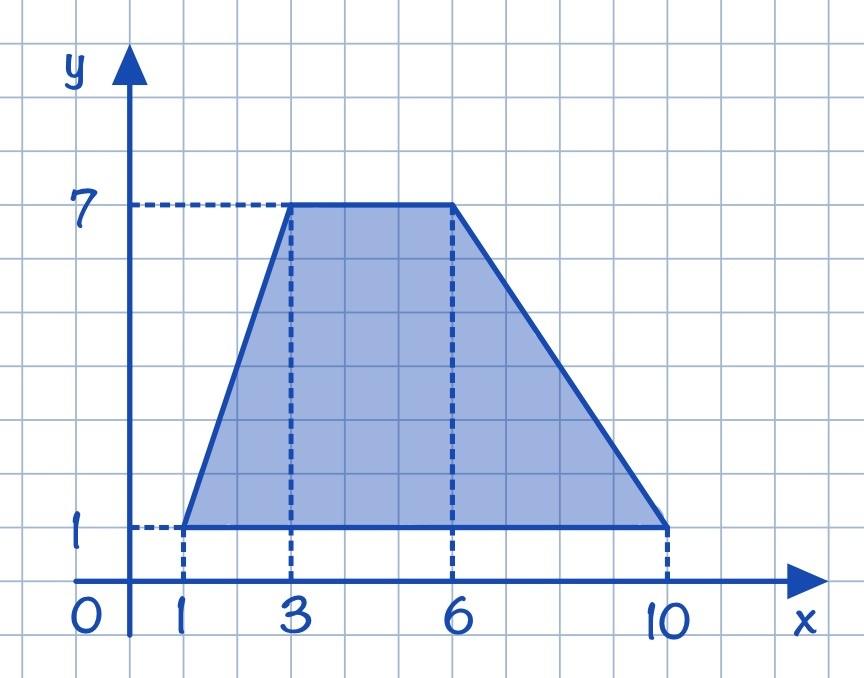
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (3;7), (6;7), (10;1).

Решение:
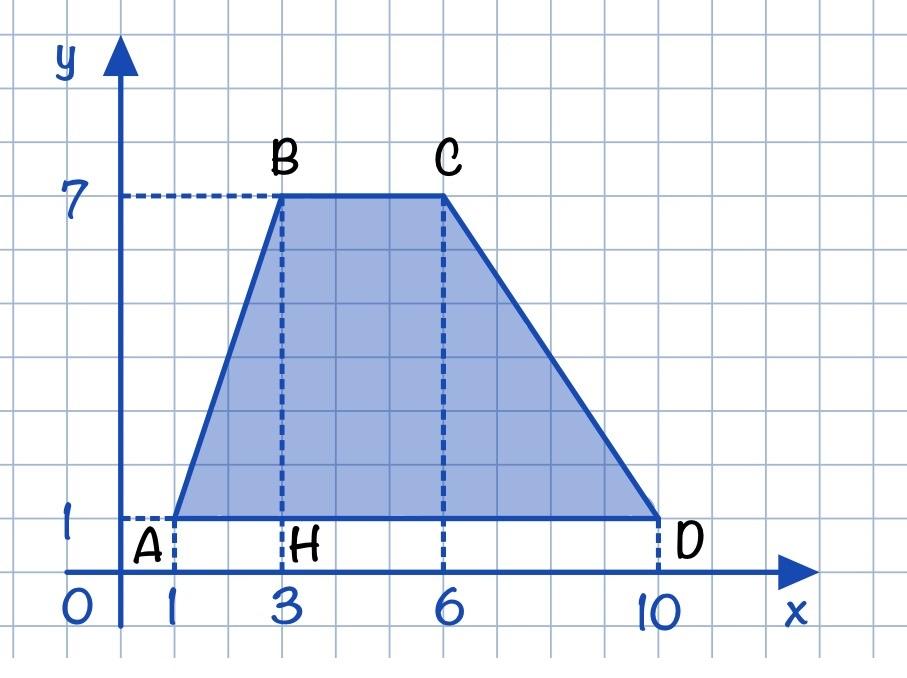
Пусть ABCD — искомая трапеция.

Площадь трапеции равна полусумме оснований, умноженной на высоту, то есть S = ½⋅(a+b)⋅h, где a,b — основания трапеции, h — высота трапеции.

В нашем случае: AD, BC — основания трапеции, BH — высота трапеции.

Найдем основание AD, оно равно разности координат по х:
AD = 10 — 1 = 9

Аналогичным образом найдем основание BC:
BC = 6 — 3 = 3

Найдем высоту BH:

BH = 7 — 1 = 6

В конечном счете получаем:
S = ½⋅(AD + BC)⋅BH
S = ½⋅(9 + 3)⋅6
S = ½⋅12⋅6
S = 6⋅6

S = 36

Ответ: 36