ЕГЭ профиль № 8
Задача на сплавы

Имеется три одинаковых по массе сплава. Известно, что меди во втором сплаве на 10% больше, чем в первом, а в третьем сплаве на 10% больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 19% меди. Сколько процентов меди содержит первый сплав?

Решение:

Пусть x% – процентное содержание меди в первом сплаве.

Тогда (x+10)% – процентное содержание меди во втором сплаве, 
(x+20)% – процентное содержание меди в третьем сплаве.

Пусть y – масса первого сплава, y – масса второго сплава и y – масса третьего сплава. Тогда 3y – масса четвертого сплава.

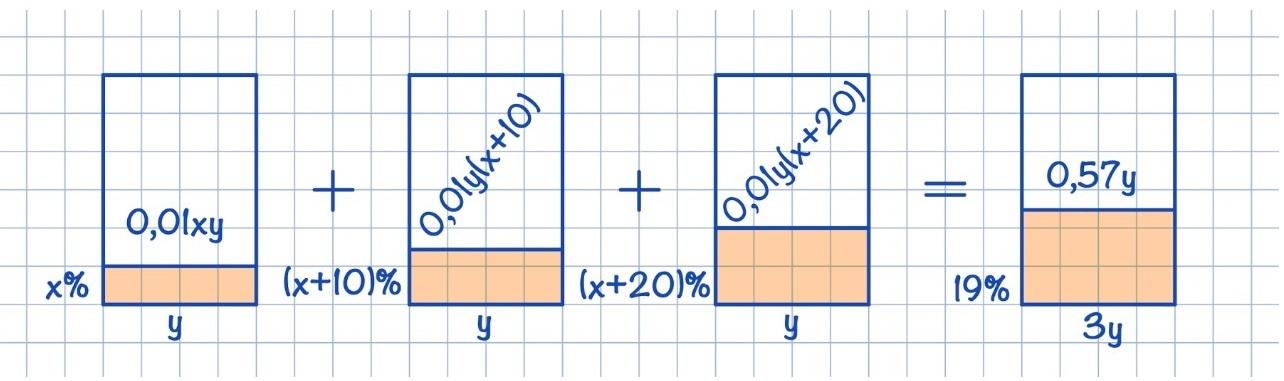
Посчитаем массу меди в первом сплаве: для этого умножим концентрацию меди на массу сплава и поделим на 100%, получим 0,01xy.

Аналогичным образом посчитаем массу меди во втором сплаве (=0,01y(x+10)), в третьем сплаве (=0,01y(x+20)) и в четвертом сплаве (=0,57y).

Составим уравнение: масса меди в трех сплавах равна массе меди в четвертом сплаве (подумайте, почему?) :

0,01xy + 0,01y(x+10) + 0,01y(x+20) = 0,57y

Домножим на 100:

xy + y(x+10) + y(x+20) = 57y

Раскроем скобки:

xy + xy + 10y + xy + 20y = 57y

Перенесем всё в левую сторону:

xy + xy +10y + xy + 20y – 57y = 0

Приведем подобные слагаемые:

3xy – 27y = 0

Поделим на 3y ≠ 0:

x – 9 = 0

В итоге получим:

x = 9

Ответ: 9 %