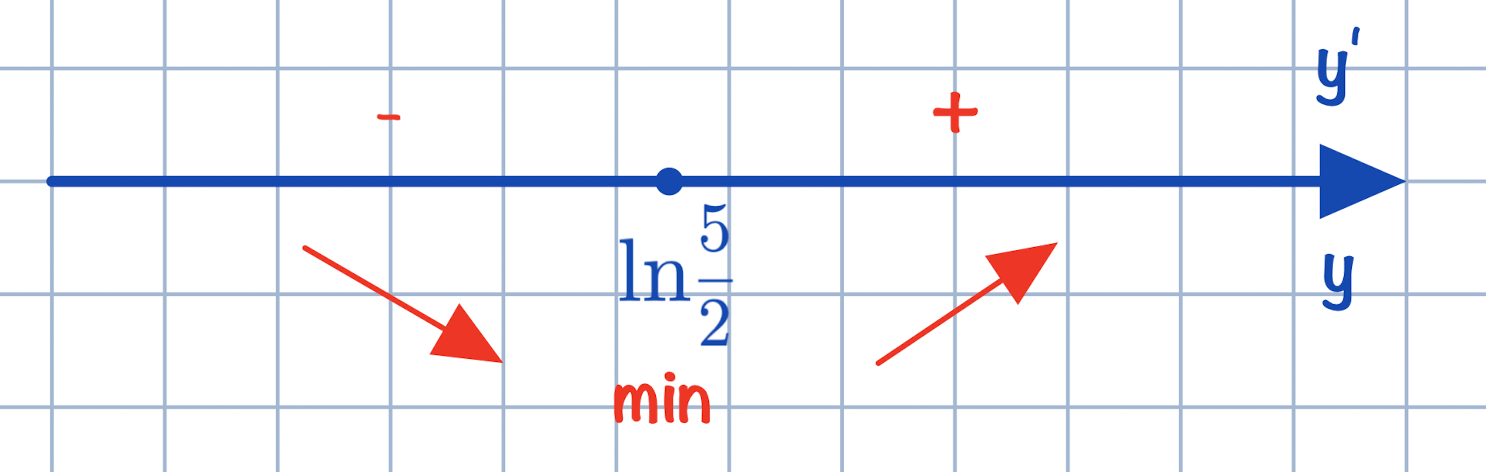ЕГЭ профиль №11
Наименьшее значение функции

Найдите наименьшее значение функции y = e²ⁿ — 5eⁿ — 2 на отрезке [-2; 1].

Решение:

В предыдущих задачах мы уже рассматривали алгоритм поиска точки минимума/максимума функции. Напомним его еще раз:

1. Найти производную;
2. Приравнять ее к нулю и решить уравнение;
3. На числовой прямой расставить знаки производной с учетом ОДЗ;
4. Расставить стрелки, характеризующие поведение функции;
5. Точка максимума — переход с возрастания функции на убывание.
   Точка минимума — переход с убывания функции на возрастание.

Наименьшее значение функции — это значение функции в точке минимума, принадлежащей заданному отрезку.

Итак, найдем производную:

Приравняем производную к нулю и решим уравнение:

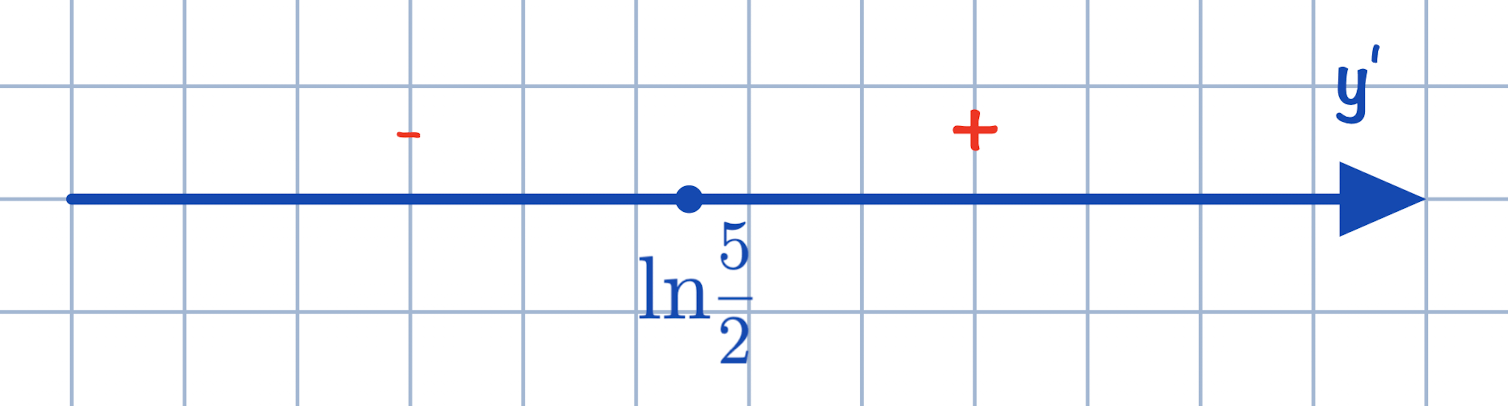
Расставим на числовой прямой знаки производной:

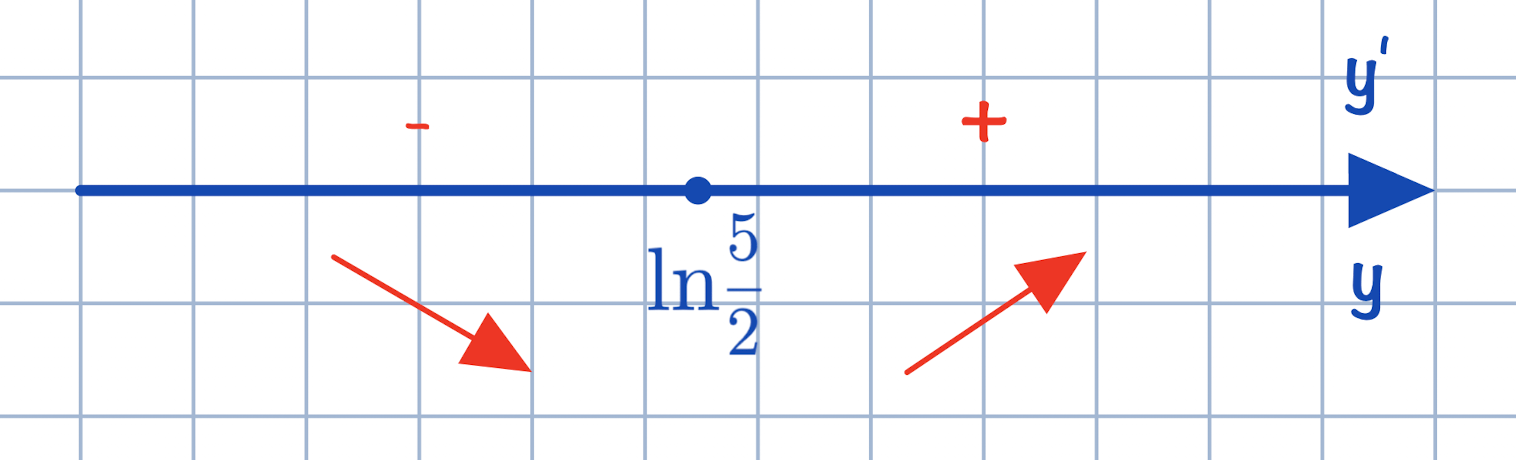
Схематично изобразим поведение функции: если функция возрастает, производная положительна; если функция убывает, производная отрицательна.

Максимум — переход с возрастания на убывание. Минимум — переход с убывания на возрастание.

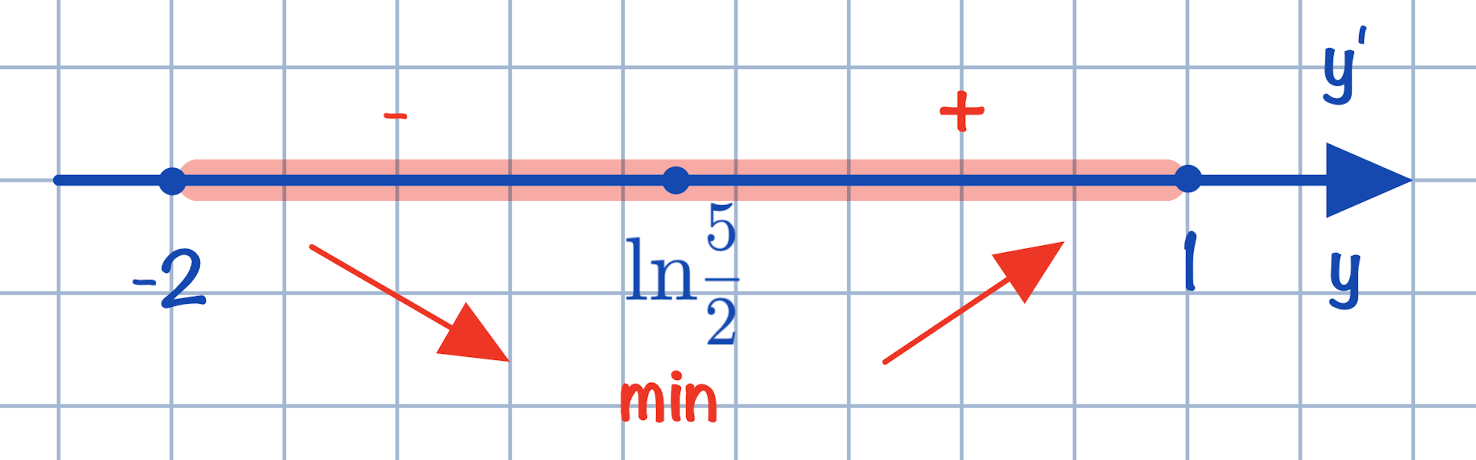
Убедимся в том, что точка минимума принадлежит отрезку, указанному в условии задачи:

Тогда наименьшее значение функции:

Ответ: -8,25