ЕГЭ профиль № 10
Теория вероятностей 2

В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трёх играх победила команда А. Какова вероятность того, что эта команда выиграет четвёртый раунд?

Решение:

Пусть 1, 2, 3, 4, 5, 6 — силы команд. Договоримся о том, что чем больше число, тем больше сила команды.

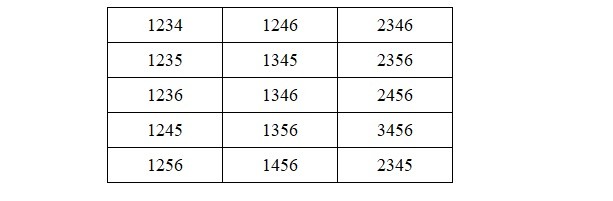
Так как в первых трех играх победила команда А, значит она была одной из сильнейших. В первых трех играх приняли участие четыре команды. Выпишем все возможные варианты:

Всего получилось пятнадцать вариантов.

Сила команды А — либо 4, либо 5, либо 6.

Пусть силы команды А равна 4.

Тогда она могла выиграть только в играх с командами, силы которых 1, 2, 3. Тогда останутся команды с силами 5 и 6, что означает, что команда А в следующем туре проиграет.

Пусть сила команды А равна 5.

Вероятность того, что команда А выиграет в первых трех раундах равна 4/15. Если команда А в следующем раунде встретится с командами 1, 2, 3, 4, то она выиграет. Если команда А в следующим раунде встретится с командой 6 — проиграет.

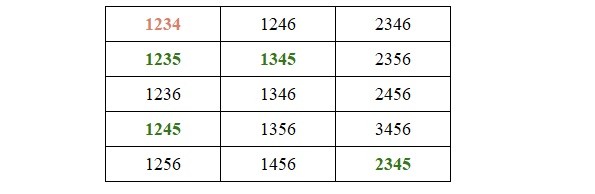
1235 => 45 или 56

1245 => 35 или 56

1345 => 25 или 56

2345 => 15 или 56

Вероятность того, что команда А выиграет, равна ½ = 0,5

Вероятность того, что выиграет команда А с силой 5, равна 4/15 ∙ 0,5 = 2/15

Пусть сила команда А равна 6.

Вероятность того, что команда А выиграет в первых трех раундах равна 10/15 = ⅔ . В следующем раунде команда А выиграет с вероятностью 1.

Итого, вероятность того, что команда А выиграет четвертый раунд, равна

2/15 + ⅔ = 2/15 + 10/15 = 12/15 = ⅘ = 0,8.

Ответ: 0,8