ЕГЭ профиль № 9
Две параболы

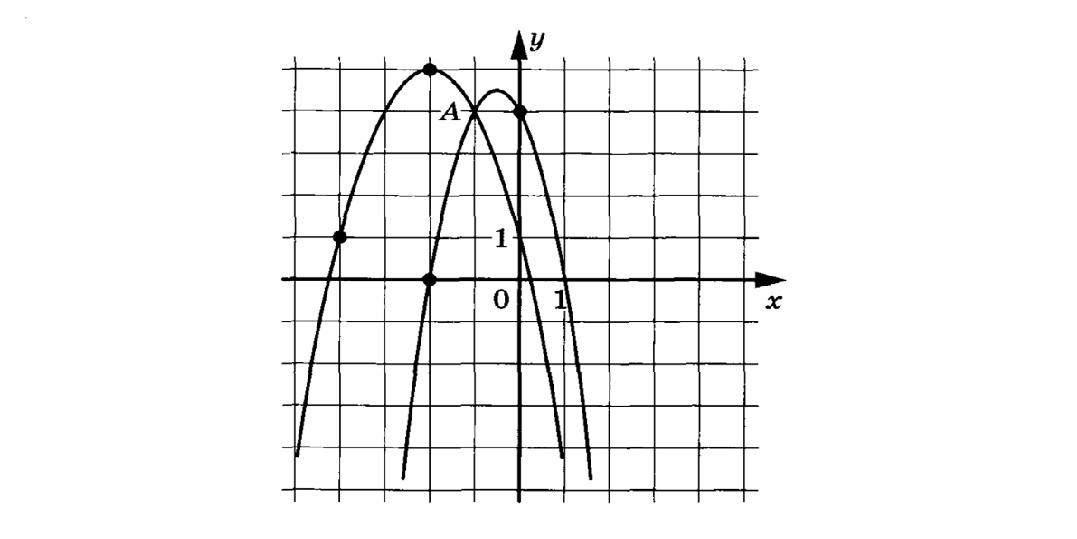
На рисунке изображены графики функций f(x)=-2x²-2x+4 и g(x)=ax²+bx+c, которые пересекаются в точках A(-1;4) и В(х₀;y₀). Найдите х₀.

Решение:

 Правая парабола пересекает ось y в точке (0;4), значит, ее уравнение задается следующей формулой: f(x)=-2x²-2x+4

Левая парабола пересекает ось y в точке (0;1), значит ее уравнение задается следующей формулой: g(x)=ax²+bx+1

Функция g(x) проходит через точку (-4;1), значит:

1=16a-4b+1

16a-4b=0

16a=4b

b=4a     (1)

Функция g(x) проходит через точку (-1;4), значит:

4=a-b+1

a-b=3     (2)

Подставим (1) в (2) и найдем а:

a-4a=3

-3a=3

a=-1

Найдем b, подставив a=-1 в (1):

b=-4

Имеем следующее:

f(x) =2x²+3x-4,

g(x) =-x²-4x+1.

Так как функции пересекаются, то f(x) = g(x):

-2x²-2x+4 = -x²-4x+1

x²-2x-3=0

D = (-2)² — 4·1·(-3) =4 + 12 = 16

x₁ = х₀ = 3 — абсцисса точки В,

x₂ = -1 — абсцисса точки А.

Ответ: 3