ЕГЭ профиль № 16
Планиметрия

В треугольнике АВС все стороны различны. Прямая, содержащая высоту ВН треугольника АВС, вторично пересекает описанную около этого треугольника окружность в точке F. Отрезок BD – диаметр этой окружности.

а) Докажите, что AD = CF.

б) Найдите DF, если радиус описанной около треугольника АВС окружности равен 12, ∠ВАС = 35°, ∠АСВ = 65°.

Решение:

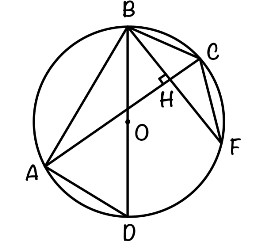
а) △ABD – прямоугольный, так как сторона BD содержит центр описанной окружности.

Пусть ∠ABD = x°, тогда ∠ADB = 90°-x°

∠ADB = ∠ACB = 90°-x° (вписанные углы, опирающиеся на одну и ту же дугу, равны)

△BCH: ∠CBH = 180°-∠BCH-∠BCH = 180°-90°-(90°-x°)=x°

Получаем, что ∠ABD = ∠CBF = x° → AD = CF (равные вписанные углы опираются на равные хорды).

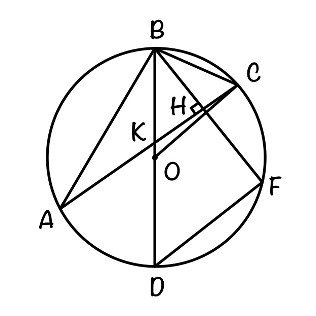
б) ∠ВОС = 2∠ВАС = 2·35° = 70° (центральный угол)

△ВОС – равнобедренный, так как ВО=СО=R → ∠CBO = (180°-∠BOC)/2 = (180°-70°)/2 = 55°

△BCH: ∠CBH = 180°-∠BHC-∠BCH = 180°-90°-65°=25°

∠FBD = ∠CBO -∠CBH = 55°-25° =30°

△FBD – прямоугольный, так как сторона BD содержит центр описанной окружности. Тогда BD = 2R = 24

Катет, лежащий напротив угла 30°, равен половине гипотенузы → FD = BD/2 = 24/2 = 12

Ответ: б) 12