ЕГЭ профиль № 16
Прямоугольный треугольник

На гипотенузе АВ и катетах ВС и АС прямоугольного треугольника АВС отмечены точки M, N и K соответственно, причём прямая NK параллельна прямой АВ и BM=BN=KN/2. Тогда P — середина отрезка KN.

а) Докажите, что четырехугольник BCPM — равнобедренная трапеция.

б) Найдите площадь треугольника АВС, если BM=1 и ∠BCM=15°.

Решение:

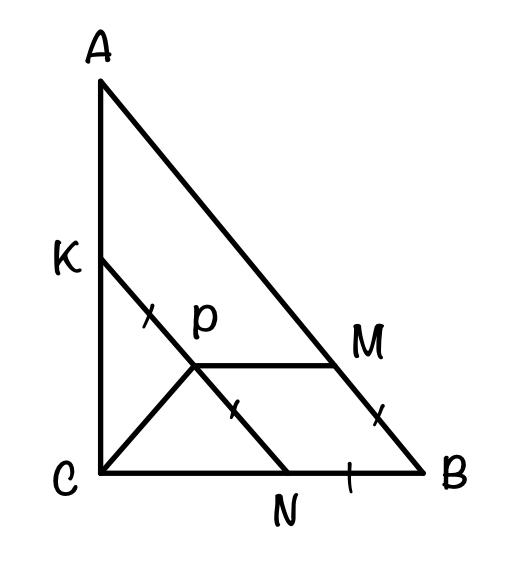
а) Т.к. P — середина KN, то KP = PN.

Тогда BN = BM = KN/2 = KP = PN.

PMBN: PN || MB (по условию), PN = MB → PMBN — параллелограмм → PM = NB и PM || NB → PM || CB

△KCP: CP — медиана, проведённая из вершины прямого угла → CP = KP = PN

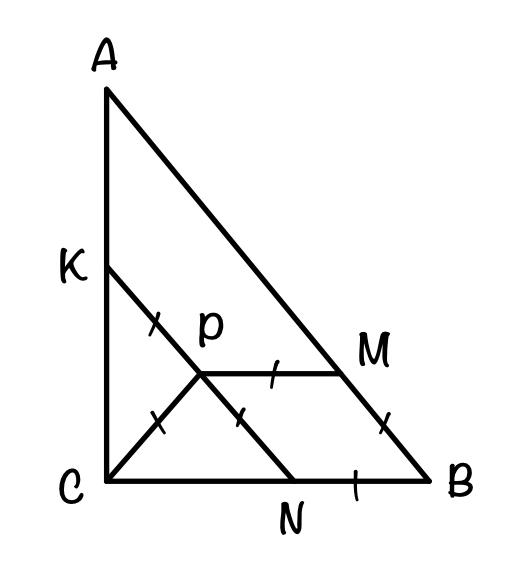
BCPM: PM || CB, CP = MB → BCPM — равнобедренная трапеция.

б)  ∠BCM = ∠CMP = 15° (как накрест лежащие при CB || PM и секущей CM)

∠CMP = ∠MCP = 15° (т.к. CP = PM → △CPM — равнобедренный треугольник)

∠CPM = 180° — ∠PCM — ∠CMP = 150°

∠PCB = ∠PCM + ∠MCB = 30°

∠CPN = ∠PNC = 30° (т.к. CP = PN → △CPN — равнобедренный треугольник)

∠PNC = ∠ ABC = 30° (как соответственные при KN || AB и секущей CB)

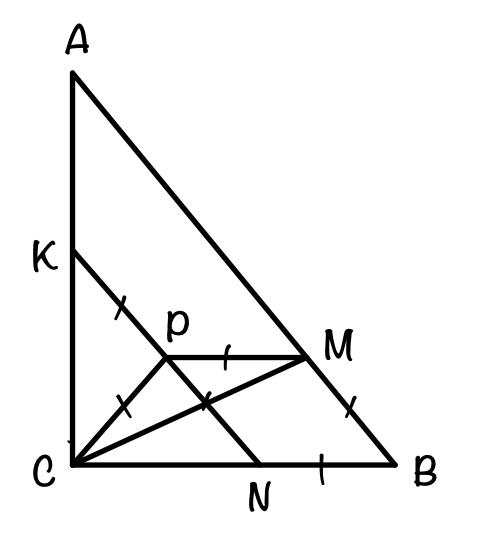
△CPM: CM² = CP² + PM² -2·CP·PM·cos∠CPM = 1 + 1 — 2·1·1·cos150° = 2+√3

△CMB: CM² = BC² +BM² -2·BC·BM·cos∠ABC = BC² +1 -2·BC·1·(√3/2)

2+√3 = BC² +1 -2·BC·1·(√3/2)

BC² — √3BC — 1 — √3 = 0

D = (√3)² — 4·1·(-1-√3) = 7 + 4√3 = (2+√3)² → BC = 1+√3

△ABC: Пусть AB=2x

sinB = AC/AB

AC = AB·sinB = 2x·(1/2) = x

AB² = AC² + BC²

4x² = x² + (1+√3)²

3x² = (1+√3)²

(√3x+1+√3)·(√3x-1-√3) = 0

x = (1+√3)/√3

S = (ACBC)/2 = (1+√3)²/(2√3) = (2√3+3)/3

Ответ: б) (2√3+3)/3