Вписанная окружность ЕГЭ профиль № 16

Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках С₁, В₁ и А₁ соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника AB₁C₁.

а) Докажите, что C₁Q — биссектриса угла АС₁В₁.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник АВ₁С₁, если известно, что ВС = 7. АВ = 15, АС = 20.

Решение:

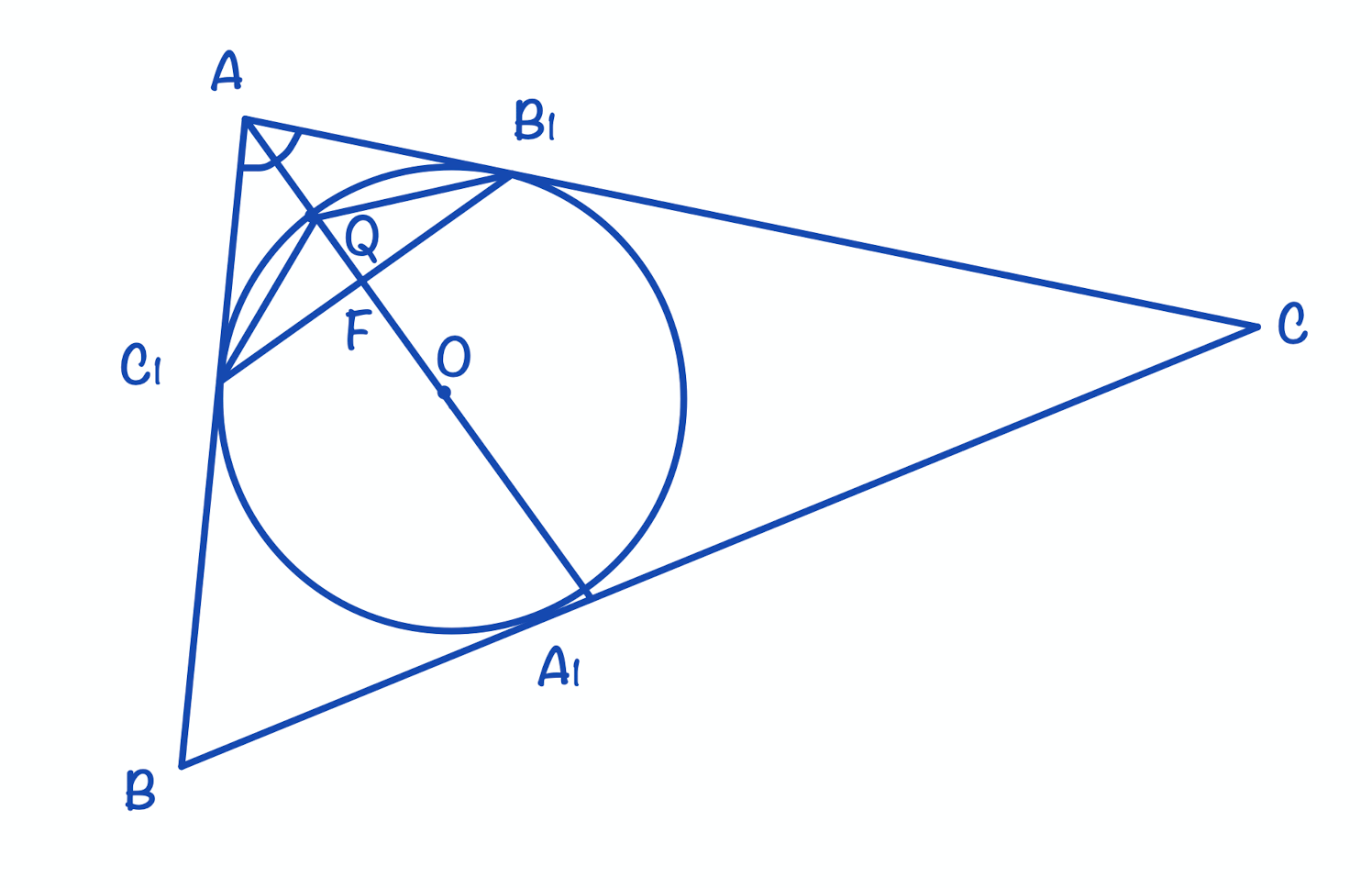
а) Касательные, проведенные к окружности из одной точки, равны. Тогда АС₁ = АВ₁.

∆АС₁F = ∆AB₁F (по двум сторонам и углу между ними: AF — общая сторона, AC₁ = AB₁, ∠FAC₁ = ∠FAB₁ — по условию). Тогда С₁F = B₁F, то есть ∆QC₁B₁ — равнобедренный треугольник.

Угол, образованный касательнoй и хордой, проходящей через точку касания, равен половине величины дуги, заключенной между его сторонами:

Касательная — AC₁

Хорда — QC₁

Дуга, заключенная между касательной и хордой, — QC₁

Тогда ∠QC₁A = ◡QC₁/2

Вписанный угол равен половине дуги, на которую он опирается: ∠QB₁F = ◡QC₁/2

Углы при основании равнобедренного треугольника равны: ∠QB₁F = ∠QС₁F

Получаем: ∠QB₁F = ∠QС₁F = ∠QC₁A = ◡QC₁/2 => QC₁ — биссектриса угла AC₁F.

б) Заметим, что AQ и C₁F пересекаются в точке Q. Известно, что центр вписанной окружности находится в точке пересечения биссектрис треугольника, то есть в точке Q. Тогда расстояние от точки О до центра окружности, вписанной в треугольник АВ₁С₁, равно отрезку OQ = r (где r — радиус окружности, вписанной в треугольник АВС)

Вспомним формулу: S = pr (p — полупериметр треугольника). Отсюда получаем, что r = S/p

По формуле Герона находим площадь треугольника АВС:

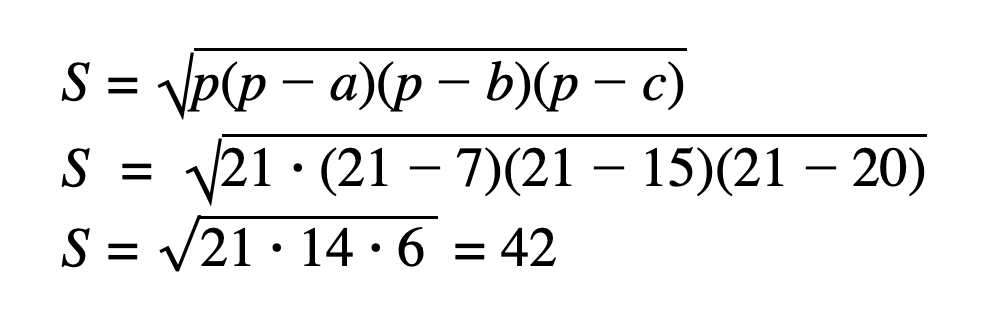
S = 42

p = 21

r = S/p = 42/21 = 2

Ответ: б) 2