ЕГЭ Профиль № 6
Разность первообразных

На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой).

Пользуясь рисунком, вычислите F(5) — F(3), где F(x) — одна из первообразных функции f(x).

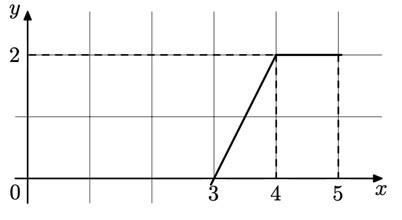
Решение:

Площадь под графиком функции f(x) на отрезке [a; b] равна разности первообразных:

S = F(b) — F(a)

Нам необходимо найти площадь закрашенной фигуры на отрезке [3; 5], то есть  a = 3; b = 5. Значит S = F(5) — F(3)

Тогда площадь закрашенной фигуры равна площади трапеции:

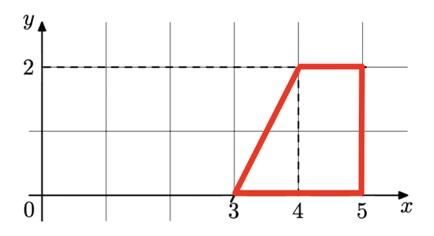
S = (1+2)⋅2/2 = 6/2 = 3

Ответ: 3